| 1) |
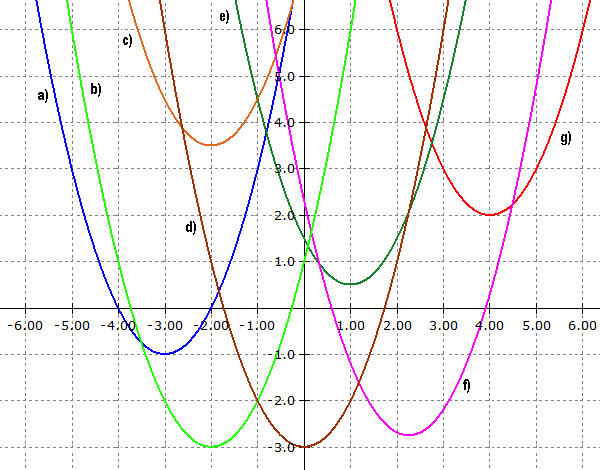
Lies die
Scheitelkoordinaten der jeweiligen Parabel aus dem
Koordinatensystem ab und gib ihre Funktionsgleichung mit und
ohne Klammern an. |
 |
| |
 |
|
| 2) |
Gib die
Koordinaten des Scheitelpunktes folgender Parabeln an. |
|
| a) |
 |
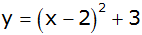b) |
 |
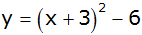c) |
 |
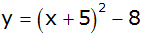| d) |
 |
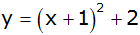e) |
 |
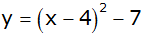f) |
 |
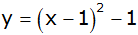| g) |
 |
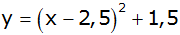h) |
 |
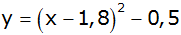i) |
 |
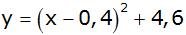| j) |
 |
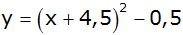k) |
 |
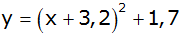l) |
 |
|
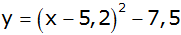| 3) |
Eine verschobene
Normalparabel hat den Scheitel S. Gib die Funktionsgleichung in
Scheitelform an. |
|
|
|
| 4) |
Gib die
Koordinaten des Scheitelpunktes folgender Parabeln an. |
|
| a) |
 |
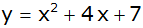b) |
 |
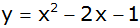c) |
 |
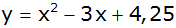| d) |
 |
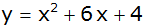e) |
 |
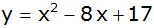f) |
 |
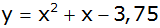| g) |
 |
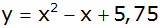h) |
 |
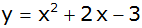i) |
 |
|
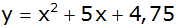| 5) |
Welcher
Scheitelpunkt gehört zu welcher Parabel? |
|
| |
|
|
| 6) |
Welcher Punkt liegt auf welcher Parabel? |
|
| |
|
|
| 7) |
Der
Punkt P liegt auf der Parabel mit
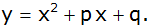Bestimme die vollständige Funktionsgleichung. |
|
|
|
| 8) |
Die
Parabel mit der Gleichung verläuft durch die Punkte A und
B. Bestimme die Funktionsgleichung und die Koordinaten des
Scheitelpunktes mit Hilfe eines linearen Gleichunssystems. |
|
|
|
| 9) |
Zeichne das Parabelpaar und lies die Koordinaten des
Schnittpunktes ab. |
|
|
|
| 10) |
Zeichne das Schaubild der Funktion, bestimme die Schnittpunkte
mit der x-Achse und gib die Nullstellen an. |
|
|
|
| 11) |
Bestimme die Lösungen der Gleichung zeichnerisch. |
|
|
|
