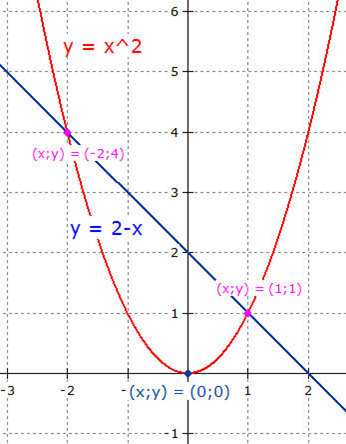
Möchte man eine quadratische Gleichung
zeichnerisch lösen, zerlegt man die Gleichung
in zwei Funktionsgleichungen.
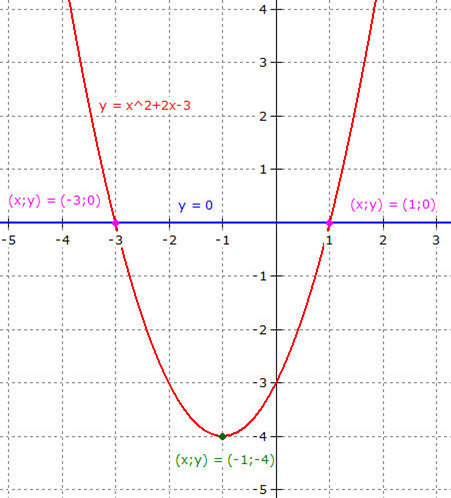
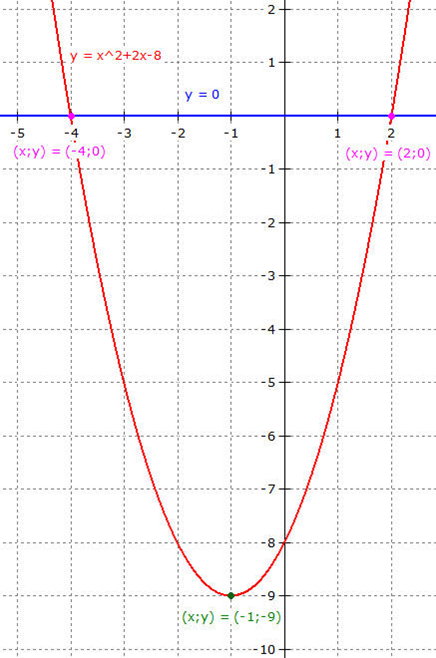
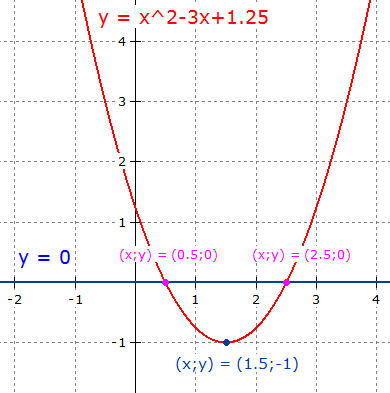
Die x-Werte der Schnittpunkte der
beiden Funktionsgleichungen sind die Lösungen
der quadratischen Gleichung.
Hat man die
Funktionsgleichung einer Parabel in der
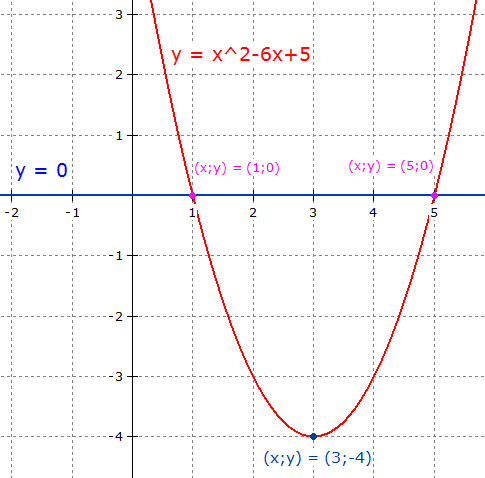
Scheitelform, so kann man die
Koordinaten des Scheitelpunktes
ablesen. Dann legt man die Schablone einer
Normalparabel in einem x,y-Koordinatensystem an
und zeichnet die Parabel. |
|
|
| a) |
 |
 |
 |
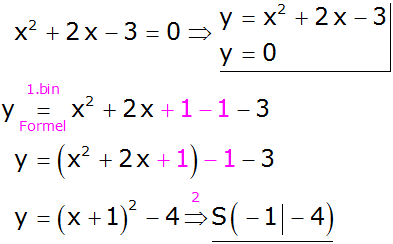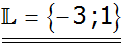| b) |
 |
 |
 |
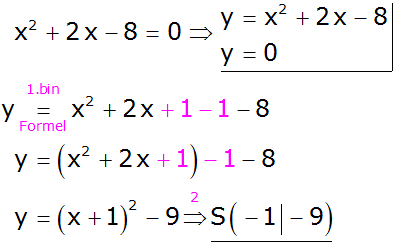| c) |
 |
 |
 |
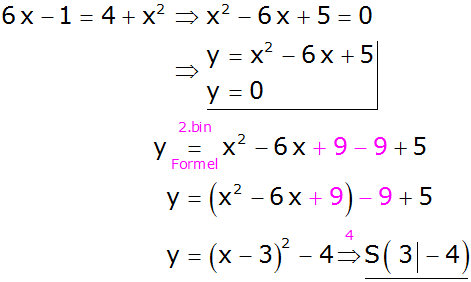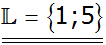| d) |
 |
 |
 |
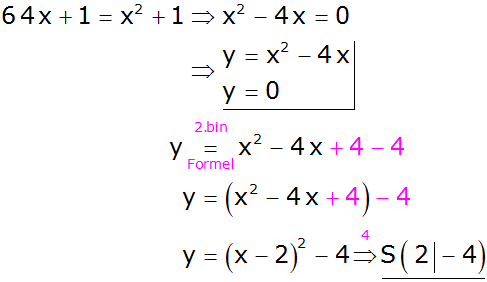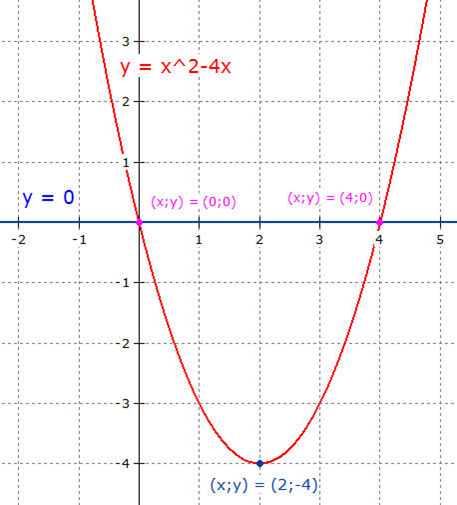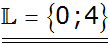| e) |
 |
 |
 |
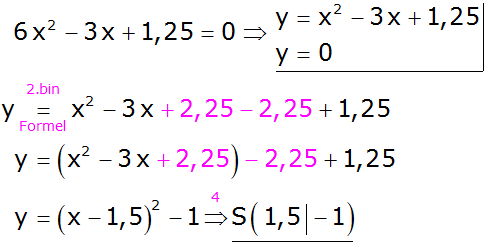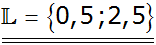| f) |
 |
 |
 |
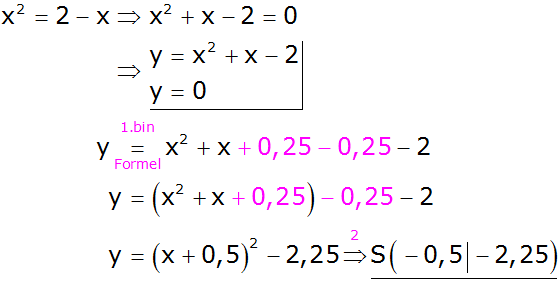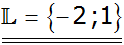| f) |
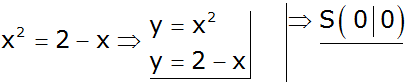
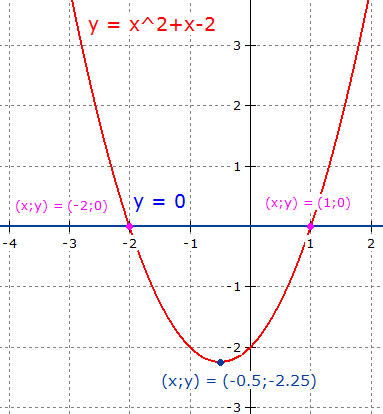
In diesem Fall hat man die Funktionsgleichung
einer Normalparabel mit dem
Scheitel
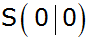und eine lineare Funktionsgleichung.
Umformung durch quadratische Ergänzung und
binomische Formel um die Scheitelform zu bestimmen ist
nicht nötig!!! |
 |
|
|
|
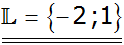