Home Geschichte Informatik Lernmaterial Linkliste Mathematik Smartphone ARS LB

2015 Übersicht

nach oben
Pflichtaufgaben
Aufgabe P1:
Im Dreieck ABC gilt:
Berechnen Sie den Umfang des Dreiecks EBC.
4 P
Aufgabe P2:
Das Viereck ABCD ist ein Quadrat.

Es gilt:
Berechnen Sie die Länge von .
4 P
Aufgabe P3:
Ein Kegel ist teilweise mit Wasser gefüllt. Dabei nimmt das Wasser die Hälfte des Kegelvolumens ein. Dieses Wasser soll vollständig in eine quadratische Pyramide umgefüllt werden.

Es gilt:
Läuft das Wasser über?
Überprüfen Sie durch Rechnung.
3,5 P
Aufgabe P4:
In einem Behälter liegen 20 Kugeln. Sie sind rot, blau und grün gefärbt.
Es werden zwei Kugeln gleichzeitig gezogen.

Im Baumdiagramm fehlt eine Wahrscheinlichkeitsangabe.
Ergänzen Sie diese.

Wie groß ist die Wahrscheinlichkeit, höchstens eine grüne Kugel zu ziehen?

In einem anderen Behälter liegen von jeder Farbe doppelt so viele Kugeln. Es werden ebenfalls zwei Kugeln gleichzeitig gezogen.

Uli sagt: "Die Wahrscheinlichkeit, höchstens eine grüne Kugel zu ziehen, ist gleich."

Hat Uli Recht?
Begründen Sie durch Rechnung.
4 P
Aufgabe P5:
Das Schaubild zeigt die Ausschnitte von vier Parabeln.

Welcher Graph gehört zur angegebenen Wertetabelle?
Begründen Sie Ihre Entscheidung.
x 0 1 2 3
y 1 0 -3 -8
 
Berechnen Sie die Koordinaten des Schnittpunktes Q der beiden verschobenen Normalparabeln und .
 
Wie heißt die Gleichung der Parabel ?
Entnehmen Sie dazu erforderliche Werte aus dem Schaubild.
4 P
Aufgabe P6:

Lösen Sie das Gleichungssystem:
  3 P
Aufgabe P7:

Das Diagramm zeigt den Wert der Aktie "Motelo" jeweils am Jahresende.

Um wieviel Prozent ist der Wert der Aktie von 2010 bis 2013 insgesamt angestiegen?

Am Ende des Jahres 2014 lag der Wert der Aktie 15,4% über dem Wert am Ende des Jahres 2013.

Zeichnen Sie im Diagramm den Jahresendwert von 2014 ein.

Welchen jährlich gleichbleibenden Zinssatz hätte eine Bank bieten müssen, um von 2009 bis 2013 den gleichen Wertzuwachs zu erzielen?
  3,5 P
Aufgabe P8:
Die Klassen 10a und 10b machen einen gemeinsamen Ausflug und spielen Minigolf.
Beim Minigolf zählt jeder Schlag als Punkt.
Hat der Ball nach sechs Punkten das Ziel nicht erreicht, ist ein Zusatzpunkt anzurechnen.
Die Höchstpunktzahl an einer Bahn beträgt also sieben Punkte.

Die Diagramme und die Boxplots zeigen die Ergebnisse der beiden Klassen nach der ersten Bahn.

  

 
               

 
Zu welcher Klasse gehört der jeweilige Boxplot? Begründen Sie.
  

Wieviel Prozent der Schüler der Klasse 10a haben fünf oder mehr Punkte?
  
Überprüfen Sie folgende Aussage:  
"Die durchschnittliche Punktzahl der Klasse 10b beträgt genau vier Punkte."
  4 P
Wahlaufgaben
Aufgabe W1a:
Im Trapez ABCD gilt:  

Berechnen Sie den Winkel .

Berechnen Sie den Flächeninhalt des Dreiecks EBD.
5,5 P
Aufgabe W1b:
Von einem rechteckigen Blatt Papier wird entlang der gestrichelten Linie ein Stück abgeschnitten und an anderer Stelle angelegt (siehe Skizze).
 
Es gilt:
 
 

 

Bea behauptet:
"Das Viereck AEFG hat den gleichen Umfang wie das Rechteck ABCD."
 

 

Hat Bea Recht?
Begründen Sie Ihre Aussage rechnerisch oder durch Argumentation.
4,5 P
Aufgabe W2a:
                                                                                                                                                                                   5,5 P
Gegeben sind zwei Dreiviertelkreise.
Aus ihnen werden der Mantel eines Kegels und der Mantel einer regelmäßigen sechsseitigen Pyramide gefertigt.
 

 

Berechnen Sie die Differenz der beiden Körperhöhen.
Aufgabe W2b:
Ein zusammengesetzter Körper besteht aus einem gleichschenkligen Dreiecksprisma und einem halben Kegel (siehe Skizze).
Es gilt:
 

Berechnen Sie die Gesamtlänge k des zusammengesetzten Körpers.
4,5 P
Aufgabe W3a:
Zu einer verschobenen, nach oben geöffneten Normalparabel p gehört die unvollständig ausgefüllte Wertetabelle.
x 0 1 2 3 4 5
y 11 6     3  

Geben Sie die Gleichung der Parabel p an.

Vervollständigen Sie die Wertetabelle.

Eine Gerade g hat die Steigung m = -1 und geht durch den Punkt P(-2,5|6).
Weisen Sie rechnerisch nach, dass p und g keine gemeinsamen Punkte haben.
 

Eine Gerade h verläuft parallel zur Geraden g und geht durch den Scheitelpunkt von p.
Berechnen Sie die Koordinaten des Schnittpunktes R der Geraden h mit der x-Achse.
  5,5 P
Aufgabe W3b:
Eine Parabel der Form mit dem Scheitelpunkt schneidet die x-Achse in den Punkten und .

Eine nach oben geöffnete Normalparabel hat den Scheitelpunkt .

Die beiden Parabeln haben einen gemeinsamen Punt T.
Berechnen Sie die Koordinaten von T.

Die Punkte , und T bilden ein Dreieck.
Berechnen Sie den Flächeninhalt des Dreiecks .

Der Punkt T bewegt sich auf der Parabel oberhalb der x-Achse.
Für welche Lage von T wird der Flächeninhalt des Dreiecks am größten?
Begründen Sie Ihre Aussage rechnerisch oder durch Argumentation.
  4,5 P
Aufgabe W4a: 5,5 P
In einem Kartenstapel liegen zwölf Karten.
Die Verteilung ist in der Tabelle dargestellt.

Die Karten werden gemischt und verdeckt auf den Tisch gelegt. Zwei Karten werden gleichzeitig gezogen.

Wie groß ist die Wahrscheinlichkeit, eine rote und eine schwarze Karte zu erhalten?
Kartenfarbe
schwarz rot
Anzahl
6 1 3 2

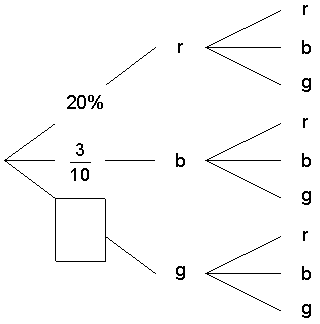
Die zwölf Karten werden für ein Glücksspiel eingesetzt. Es sollen ebenfalls zwei Karten gleichzeitig gezogen werden.

Dazu wird nebenstehender Gewinnplan geprüft.

Berechnen Sie den Erwartungswert.

Sophie macht den Vorschlag, den Gewinn für "zweimal Karo" auf 20,00 € hochzusetzen und alles andere zu belassen.
Der Betreiber des Glücksspiels protestiert und behauptet, er würde dann Verlust machen.

Hat der Betreiber Recht? Begründen Sie durch Rechnung.
Ergebnisse Gewinn
zweimal Karo 10,00 €
zweimal Herz 5,00 €
sonstige kein Gewinn
Einsatz pro Spiel: 1,00 €
Aufgabe W4b:
David und Tim messen sich im Kugelstoßen. Beim Stoß von David verlässt die Kugel
seine Hand in einer Höhe von 2,20 m (siehe Skizze):
Nach einer horizontalen Entfernung von 4,30 m hat die Kugel ihre maximale Höhe von 3,90 m erreicht.
Die Flugbahn der Kugel lässt sich annähernd durch eine Parabel mit der Funktionsgleichung beschreiben.

Welche Weite hat David erzielt?

Tim stößt die Kugel ebenfalls aus dem Stoßkreis. Die Kugel verlässt seine Hand in einer Höhe von 1,90 m.

Die Parabelgleichung für diesen Stoß lautet: .

  

Vergleichen Sie die beiden Kugelstoßweiten.
4,5 P