Home Geschichte Informatik Lernmaterial Linkliste Mathematik Smartphone ARS LB
2013 Übersicht
nach oben
Pflichtaufgaben
Aufgabe P1:
Im Trapez ABCD gilt:
Berechnen Sie die Länge der Strecke .
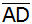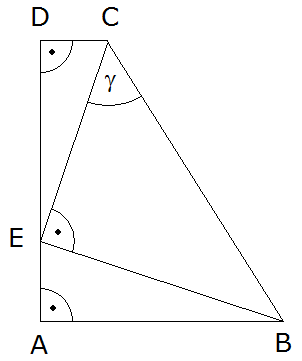4 P
Aufgabe P2:
Das rechtwinklige Dreieck AEF überdeckt das Quadrat ABCD teilweise.
Es gilt:
Berechnen Sie den Winkel und die Länge von  .
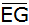4 P
Aufgabe P3:
Ein Zylinder und eine quadratische Pyramide haben gleich große Mantelflächen.
Die Umfänge der beiden Grundflächen sind ebenfalls gleich.

Für den Zylinder gilt:
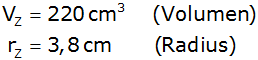Berechnen Sie die Höhe der Pyramide.
4 P
Aufgabe P4:
Lösen Sie die Gleichung:
3,5 P
Aufgabe P5:
Eine Parabel p mit der Gleichung 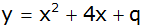geht durch den Punkt .  
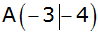Der Punkt liegt ebenfalls auf der Parabel p.  
Berechnen Sie die y-Koordinate des Punktes B.  
   
Die Gerade g geht durch den Scheitelpunkt S von p und durch den Punkt B.  
Bestimmen Sie die Gleichung der Geraden g.
3,5 P
Aufgabe P6:
Frau Wagner möchte einen Betrag von 5 000,00 € für drei Jahre anlegen.
Das Bankhaus Adler wirbt mit folgendem Angebot:
Im Beratungsgespräch bietet das Bankhaus Adler an, dass Frau Wagner nach Ablauf der drei Jahre zusätzlich eine Bonusprämie in Höhe von 100,00 € erhält.
Welchen Gesamtbetrag würde das Bankhaus Adler nach Ablauf der drei Jahre einschließlich Bonusprämie ausbezahlen?
Zusätzlich lässt sich Frau Wagner von der Opti-Bank beraten. Ihr wird ein jährlich gleichbleibender Zinssatz angeboten. Zinsen werden mitverzinst. Eine Bonusprämie wird nicht vereinbart.
Wie hoch müsste der jährlich gleichbleibende Zinssatz für die drei Jahre bei der Opti-Bank mindestens sein, damit sich Frau Wagner für dieses Angebot entscheidet?
3,5 P
Aufgabe P7:
In einer Schale liegen gleich aussehende Schokowürfel.
Sechs Schokowürfel sind mit Marzipan, vier mit Nougat und zwei mit Karamel gefüllt.
Anstasia zieht gleichzeitig zwei Schokowürfel.

Mit welcher Wahrscheinlichkeit zieht sie zwei Schokowürfel mit unterschiedlichen Füllungen?

In einer anderen Schale liegen von jeder Sorte halb so viele Schokowürfel (dreimal Marzipan, zweimal Nougat, einmal Karamel).
Leon zieht ebenfalls zwei Schokowürfel mit einem Griff.
Er behauptet: "Die Wahrscheinlichkeit, zwei Schokowürfel mit unterschiedlichen Füllungen zu ziehen, bleibt gleich."

Hat Leon Recht? Begründen Sie durch Rechnung.
4 P
Aufgabe P8:
Drei Jugendgruppen wurden über den Zeitraum von einer Woche nach ihren Online-Zeiten bei der Nutzung "Sozialer Netzwerke" befragt.
Dabei ergaben sich folgende Zeitangaben in Minuten.
  
 

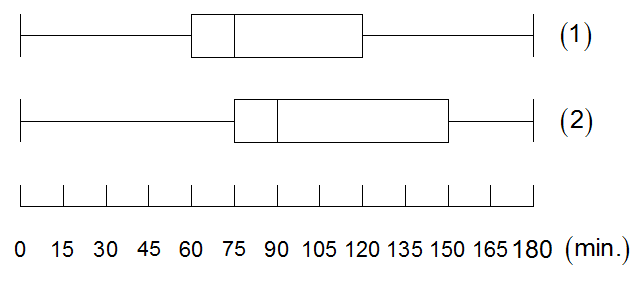
Zu welchen Gruppen gehören die beiden abgebildeten Boxplots?
Begründen Sie Ihre Antwort.
  
 

Erstellen Sie für die dritte Gruppe den fehlenden Boxplot.
3,5 P
Wahlaufgaben
Aufgabe W1a:
Im rechtwinkligen Dreieck ABC liegt das gleichschenklige Dreieck ADE.  
Es gilt:

Berechnen Sie den Winkel .

Berechnen Sie den Umfang des Dreiecks AEC.
6 P
Aufgabe W1b:
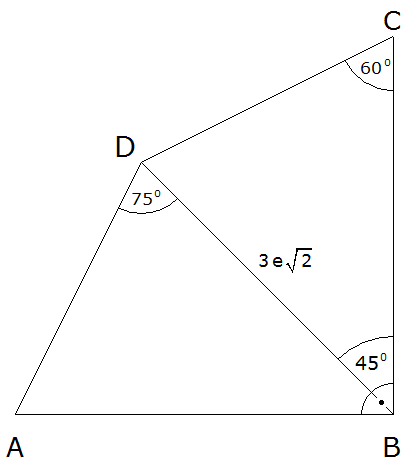
Gegeben ist das Viereck ABCD.

Weisen Sie ohne Verwendung gerunderter Werte nach, dass der Flächeninhalt des Vierecks ABCD mit der Formel

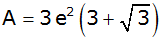berechnet werden kann.
4 P
Aufgabe W2a:
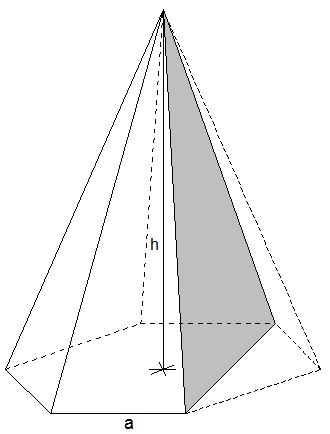
Von einer massiven regelmäßigen sechsseitigen Pyramide sind bekannt:
a = 3,4 cm
h = 6,7 cm


Ein Teil der Pyramide wird abgeschnitten (siehe Skizze).

Berechnen Sie die Mantelfläche des neu entstandenen Körpers.
5 P
Aufgabe W2b:
Die Skizze zeigt die Achsenschnitte eines Zylinders und eines Doppelkegels (zwei gleich große Kegel mit gemeinsamer Grundfläche).

Die Schnittflächen der beiden Körper sind gleich große Quadrate mit einem Flächeninhalt von jeweils .

Um wie viel Prozent unterscheiden sich die Oberflächen der beiden Körper?
5 P
Aufgabe W3a:
Das Schaubild zeigt einen Ausschnitt einer verschobenen Normalparabel .
Der Punkt R liegt auf .

Die unvollständig ausgefüllte Wertetabelle gehört zur Normalparabel .
x 3 4 5 6 7 8 9
y         - 4    

Geben Sie die Funktionsgleichung der Parabel an und füllen Sie die Wertetabelle vollständig aus.

Die Parabel hat die Gleichung . Weisen Sie rechnerisch nach, dass die beiden Parabeln keinen gemeinsamen Punkt haben.

Geben Sie die Gleichung einer Geraden an, die keinen gemeinsamen Punkt mit den beiden Parabeln hat.
5 P
Aufgabe W3b:
Die Parabel hat die Gleichung .
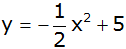Die nach oben geöffnete und verschobene Normaparabel 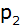hat den Scheitel .
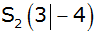Der Scheitel von sowie die Schnittpunkte 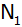und von 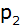mit der x-Achse bilden ein Dreieck.
Berechnen Sie den Flächeninhalt des Dreiecks .
Eine Gerade g geht durch die Schnittpunkte der beiden Parabeln und teilt somit die Fläche des Dreiecks.
Überprüfen Sie, ob die Gerade g die Fläche des Dreiecks halbiert.
5 P
Aufgabe W4a:
Die beiden Netze zeigen die Augenzahlen zweier besonderer Spielwürfel.

Beide Spielwürfel werden gleichzeitig geworfen.

Wie groß ist die Wahrscheinlichkeit mindestens eine "Sechs" zu werfen?

Die beiden Würfel werden für ein Glücksspiel eingesetzt.
Dazu wird nebenstehender Gewinnplan geprüft.

Berechnen Sie den Erwartungswert.

Der Veranstalter des Glückspiels möchte beim Würfelnetz die "Fünf" durch eine "Sechs" ersetzen. Der Gewinnplan soll gleich bleiben.

Wäre dies für ihn vorteilhaft? Begründen Sie.
6 P
Aufgabe W4b:
Die Grafik zeigt die Lanxess Arena in Köln.
Sie wird von einem parabelförmigen Bogen überspannt. Dieser lässt sich mit der Gleichung beschreiben.
Der Bogen hat am Boden eine Spannweite von 190 m.
Die maximale Höhe des Bogens beträgt 76 m über dem Boden.

Geben Sie die Gleichung der zugehörigen Parabel an.

An einem Punkt P des Bogens, der sich in 50 m Höhe befindet, soll eine Befestigung angebracht werden.

Wie weit ist dieser Punkt P vom höchsten Punkt des Bogens entfernt?
4 P