|
Aufgabe 1a: |
Das erste Glied
einer arithmetischen Reihe beträgt 12 und das letzte
Glied 100, die Summe aller Glieder
ist 672. |
|
Aus wieviel Gliedern besteht die Reihe und wie groß
ist die Differenz? |
|
|
4 P |
|
|
Aufgabe 1b: |
Die Summe aller
Glieder einer arithmetischen Reihe beträgt 560, das
erste Glied beträgt 20 und ist
um 12 größer als
die Differenz dieser Reihe. |
|
Aus wieviel Gliedern besteht die Reihe und wie groß
ist ihr letztes Glied? |
|
|
4 P |
|
|
Aufgabe 1c: |
Eine aus 13 Gliedern bestehende arithmetische Reihe
besitzt die Summe 780, ihr letztes Glied beträgt
108.
Wird das erste Glied dieser Reihe gestrichen
und werden alle übrigen Glieder um den gleichen
Betrag k erhöht,
so besitzt sie wieder die Summe
780. |
|
Der Wert der Größe k ist zu berechnen. |
|
|
3 P |
|
|
Aufgabe 2a: |
| Es sind fünf
Zahlenfolgen durch ihre ersten drei Glieder gegeben: |
|
|
Welche dieser Zahlenfolgen sind arithmetisch bzw.
geometrisch und wie groß sind die Differenz d
bzw. der Quotient q? |
|
|
4 P |
|
|
Aufgabe 2b: |
| Es sind fünf
Zahlenfolgen durch ihre ersten drei Glieder gegeben: |
|
|
|
Es ist für jede Zahlenfolge ein in n variabler Term
für das jeweils letzte Glied zu entwickeln. |
|
|
4 P |
|
|
Aufgabe 2c: |
| Es sind fünf
Zahlenfolgen durch ihre ersten drei Glieder gegeben: |
|
|
|
Das wievielte Glied jeder Zahlenfolge beträgt 1000? |
|
|
3 P |
|
|
Aufgabe 3a: |
Bei einem
gleichschenkligen Dreieck 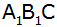 mit dem
Flächeninhalt mit dem
Flächeninhalt
 ist die Grundseite
ist die Grundseite
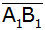 genau
genau
so lang wie die Höhe auf dieser Seite.
Parallel zur Grundseite wird ein Viertel der Fläche
des Dreiecks in Form
eines gleichschenkligen
Trapezes abgeschnitten. Von dem dadurch entstehenden
Dreieck
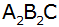 wird auf die
wird auf die
gleiche Weise wieder ein Viertel der
Fläche abgeschnitten usw. |
|
Fertige eine Skizze des geometrischen Sachverhaltes
an. |
|
|
1 P |
|
|
Aufgabe 3b: |
Bei einem
gleichschenkligen Dreieck 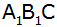 mit dem
Flächeninhalt mit dem
Flächeninhalt
 ist die Grundseite
ist die Grundseite
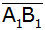 genau
genau
so lang wie die Höhe auf dieser Seite.
Parallel zur Grundseite wird ein Viertel der Fläche
des Dreiecks in Form
eines gleichschenkligen
Trapezes abgeschnitten. Von dem dadurch entstehenden
Dreieck
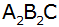 wird auf die
wird auf die
gleiche Weise wieder ein Viertel der
Fläche abgeschnitten usw. |
Stelle das Bildungsgesetz für den Flächeninhalt
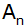 eines beliebigen Dreiecks
eines beliebigen Dreiecks
 der Folge auf und bestimme
der Folge auf und bestimme
den Flächeninhalt des
10. Dreiecks. |
|
|
3 P |
|
|
Aufgabe 3c: |
Bei einem
gleichschenkligen Dreieck 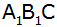 mit dem
Flächeninhalt mit dem
Flächeninhalt
 ist die Grundseite
ist die Grundseite
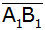 genau
genau
so lang wie die Höhe auf dieser Seite.
Parallel zur Grundseite wird ein Viertel der Fläche
des Dreiecks in Form
eines gleichschenkligen
Trapezes abgeschnitten. Von dem dadurch entstehenden
Dreieck
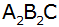 wird auf die
wird auf die
gleiche Weise wieder ein Viertel der
Fläche abgeschnitten usw. |
Beim wievielten Dreieck wird der Flächeninhalt zum
ersten Male kleiner als
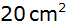 sein?
sein? |
|
|
2 P |
|
|
Aufgabe 3d: |
Bei einem
gleichschenkligen Dreieck
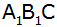 mit dem Flächeninhalt
mit dem Flächeninhalt
 ist die Grundseite
ist die Grundseite
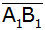 genau
genau
so lang wie die Höhe auf dieser Seite.
Parallel zur Grundseite wird ein Viertel der Fläche
des Dreiecks in Form
eines gleichschenkligen
Trapezes abgeschnitten. Von dem dadurch entstehenden
Dreieck
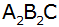 wird auf die
wird auf die
gleiche Weise wieder ein Viertel der
Fläche abgeschnitten usw. |
Berechne die Höhe des Dreiecks
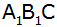 ,
bestimme unter den gegebenen Voraussetzungen die
Höhe im Dreieck ,
bestimme unter den gegebenen Voraussetzungen die
Höhe im Dreieck
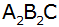 und stelle das Bildungsgesetz für die Höhe
und stelle das Bildungsgesetz für die Höhe
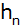 eines beliebigen Dreiecks
eines beliebigen Dreiecks
 der Folge auf.
der Folge auf. |
|
|
2 P |
|
|
Aufgabe 4a: |
Ein
zusammengesetzter Körper besteht aus einem
Kegelstumpf, dem an der kleineren Deckfläche ein
radiusgleicher Zylinder aufgesetzt ist. Die
Endflächen des Kegelstumpfes haben die Radien
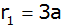 und
und
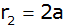 ;
die Höhe des Kegelstumpfes ist ;
die Höhe des Kegelstumpfes ist
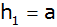 und die des Zylinders
und die des Zylinders
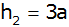 . . |
Zeichne einen Achsenschnitt des Körpers für
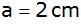 . . |
|
|
1 P |
|
|
Aufgabe 4b: |
Ein
zusammengesetzter Körper besteht aus einem
Kegelstumpf, dem an der kleineren Deckfläche ein
radiusgleicher Zylinder aufgesetzt ist. Die
Endflächen des Kegelstumpfes haben die Radien
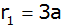 und
und
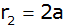 ;
die Höhe des Kegelstumpfes ist ;
die Höhe des Kegelstumpfes ist
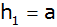 und die des Zylinders
und die des Zylinders
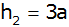 . . |
Wie groß ist die Oberfläche des Körpers als Funktion
von a und für
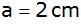 ? ? |
|
|
2 P |
|
|
Aufgabe 4c: |
Ein
zusammengesetzter Körper besteht aus einem
Kegelstumpf, dem an der kleineren Deckfläche ein
radiusgleicher Zylinder aufgesetzt ist. Die
Endflächen des Kegelstumpfes haben die Radien
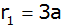 und
und
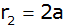 ;
die Höhe des Kegelstumpfes ist ;
die Höhe des Kegelstumpfes ist
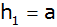 und die des Zylinders
und die des Zylinders
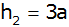 . . |
Wie groß ist das Volumen des Körpers als Funktion
von a und für
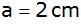 ? ? |
|
|
2 P |
|
|
Aufgabe 4d: |
Ein
zusammengesetzter Körper besteht aus einem
Kegelstumpf, dem an der kleineren Deckfläche ein
radiusgleicher Zylinder aufgesetzt ist. Die
Endflächen des Kegelstumpfes haben die Radien
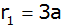 und
und
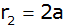 ;
die Höhe des Kegelstumpfes ist ;
die Höhe des Kegelstumpfes ist
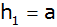 und die des Zylinders
und die des Zylinders
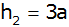 . . |
|
Aus diesem Körper wird ein achsengleicher Zylinder
ausgebohrt, der das gesamte Volumen halbiert. |
|
Wie groß ist der Bohrungsradius r? |
|
|
2 P |
|
|
Aufgabe 5a: |
Dem Inkreis
eines Quadrates mit der Seitenlänge a = 12 cm ist
ein gleichseitiges Dreieck einbeschrieben,
dessen
Grundseite parallel zu einer Quadratseite verläuft.
Durch Drehung dieser drei Flächen um die gemeinsame
Achse entstehen ein Zylinder, eine Kugel und ein
Kegel. |
|
Fertige eine Zeichnung dieser drei Flächen an. |
|
|
1 P |
|
|
Aufgabe 5b: |
Dem Inkreis
eines Quadrates mit der Seitenlänge a = 12 cm ist
ein gleichseitiges Dreieck einbeschrieben,
dessen
Grundseite parallel zu einer Quadratseite verläuft.
Durch Drehung dieser drei Flächen um die gemeinsame
Achse entstehen ein Zylinder, eine Kugel und ein
Kegel. |
Es ist nachzuweisen, dass das Dreieck die
Seitenlänge
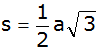 und die Höhe
und die Höhe
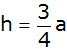 besitzt.
besitzt. |
|
|
2 P |
|
|
Aufgabe 5c: |
Dem Inkreis
eines Quadrates mit der Seitenlänge a = 12 cm ist
ein gleichseitiges Dreieck einbeschrieben,
dessen
Grundseite parallel zu einer Quadratseite verläuft.
Durch Drehung dieser drei Flächen um die gemeinsame
Achse entstehen ein Zylinder, eine Kugel und ein
Kegel. |
|
Berechne die Oberflächen der drei Drehkörper sowie
den Radius der Kugel, deren Oberfläche gleich dem
arithmetischen Mittel der vorher berechneten drei
Oberflächen ist. |
|
|
3 P |
|
|
Aufgabe 5d: |
Dem Inkreis
eines Quadrates mit der Seitenlänge a = 12 cm ist
ein gleichseitiges Dreieck einbeschrieben,
dessen
Grundseite parallel zu einer Quadratseite verläuft.
Durch Drehung dieser drei Flächen um die gemeinsame
Achse entstehen ein Zylinder, eine Kugel und ein
Kegel. |
Leite Terme für die Rauminhalte der drei Drehkörper
als Funktion von a her und zeige, dass diese im
Verhältnis 48 : 32 : 9 stehen. |
|
|
2 P |
|
|
Aufgabe 6a: |
Auf einer Karte im Maßstab 1 : 25.000
ist eine Bergspitze A eingezeichnet, die
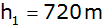 über NN liegt. Die Entfernung zu einer
anderen Bergspitze B beträgt nach der Karte
über NN liegt. Die Entfernung zu einer
anderen Bergspitze B beträgt nach der Karte
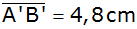 (siehe nebenstehende Abbildung).
(siehe nebenstehende Abbildung).
Um die
Höhe des Berges B zu bestimmen, misst man
von einem Punkt C, der auf der waagrechten
Strecke
 liegt und
liegt und
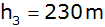 über NN liegt, die Winkel
über NN liegt, die Winkel
 und
und
 . . |
Wie groß ist die wahre Entfernung
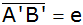 ? ? |
|
 |
|
|
2 P |
|
|
Aufgabe 6b: |
Auf einer Karte im Maßstab 1 : 25.000
ist eine Bergspitze A eingezeichnet, die
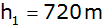 über NN liegt. Die Entfernung zu einer
anderen Bergspitze B beträgt nach der Karte
über NN liegt. Die Entfernung zu einer
anderen Bergspitze B beträgt nach der Karte
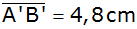 (siehe nebenstehende Abbildung).
(siehe nebenstehende Abbildung).
Um die
Höhe des Berges B zu bestimmen, misst man
von einem Punkt C, der auf der waagrechten
Strecke
 liegt und
liegt und
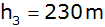 über NN liegt, die Winkel
über NN liegt, die Winkel
 und
und
 . . |
| Fertige eine genaue
Konstruktionszeichnung im Maßstab 1 : 10.000
an. |
|
 |
|
|
3 P |
|
|
Aufgabe 6c: |
Auf einer Karte im Maßstab 1 : 25.000
ist eine Bergspitze A eingezeichnet, die
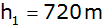 über NN liegt. Die Entfernung zu einer
anderen Bergspitze B beträgt nach der Karte
über NN liegt. Die Entfernung zu einer
anderen Bergspitze B beträgt nach der Karte
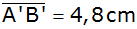 (siehe nebenstehende Abbildung).
(siehe nebenstehende Abbildung).
Um die
Höhe des Berges B zu bestimmen, misst man
von einem Punkt C, der auf der waagrechten
Strecke
 liegt und
liegt und
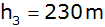 über NN liegt, die Winkel
über NN liegt, die Winkel
 und
und
 . . |
Berechne die
Entfernung
 und die Höhe
und die Höhe
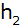 der Bergspitze B über NN.
der Bergspitze B über NN. |
|
 |
|
|
3 P |
|
|
Aufgabe 6d: |
Auf einer Karte im Maßstab 1 : 25.000
ist eine Bergspitze A eingezeichnet, die
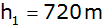 über NN liegt. Die Entfernung zu einer
anderen Bergspitze B beträgt nach der Karte
über NN liegt. Die Entfernung zu einer
anderen Bergspitze B beträgt nach der Karte
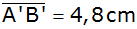 (siehe nebenstehende Abbildung).
(siehe nebenstehende Abbildung).
Um die
Höhe des Berges B zu bestimmen, misst man
von einem Punkt C, der auf der waagrechten
Strecke
 liegt und
liegt und
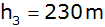 über NN liegt, die Winkel
über NN liegt, die Winkel
 und
und
 . . |
Unter welchem
Höhenwinkel
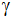 sieht man B von A aus und wie groß ist der
Abstand a zwischen A und B.
sieht man B von A aus und wie groß ist der
Abstand a zwischen A und B. |
|
 |
|
|
2 P |
|
|
Aufgabe 7a: |
|
Ein gleichschenkliges Trapez hat folgende Maße: |
Grundseite
 ,
Schenkel ,
Schenkel 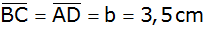 ,
Diagonale ,
Diagonale
 . . |
Konstruiere das Trapez, berechne seine Winkel und zeige,
dass die Seite
 halb so
lang wie die Seite a ist. halb so
lang wie die Seite a ist. |
|
3 P |
|
|
Aufgabe 7b: |
|
Ein gleichschenkliges Trapez hat folgende Maße: |
Grundseite
 ,
Schenkel ,
Schenkel 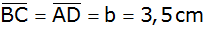 ,
Diagonale ,
Diagonale
 . . |
Wie groß ist die Entfernung e des Punktes D von der
Diagonalen
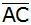 ? ? |
|
2 P |
|
|
Aufgabe 7c: |
|
Ein gleichschenkliges Trapez hat folgende Maße: |
Grundseite
 ,
Schenkel ,
Schenkel 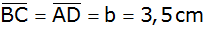 ,
Diagonale ,
Diagonale
 . . |
Begründe, dass ein gleichschenkliges Trapez einen Umkreis
besitzt, konstruiere den Mittelpunkt M
dieses Umkreises
und berechne dessen Radius r. |
|
2 P |
|
|
Aufgabe 8a: |
Ein Dreieck ABC ist durch die beiden Seiten
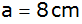 und und
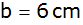 sowie
den eingeschlossenen Winkel sowie
den eingeschlossenen Winkel
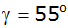 gegeben.
gegeben. |
|
Konstruiere das Dreieck. |
|
1 P |
|
|
Aufgabe 8b: |
Ein Dreieck ABC ist durch die beiden Seiten
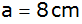 und und
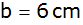 sowie
den eingeschlossenen Winkel sowie
den eingeschlossenen Winkel
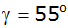 gegeben.
gegeben. |
Berechne die Seite c und die beiden Winkel
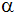 und und
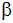 . . |
|
2 P |
|
|
Aufgabe 8c: |
Ein Dreieck ABC ist durch die beiden Seiten
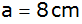 und und
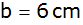 sowie
den eingeschlossenen Winkel sowie
den eingeschlossenen Winkel
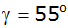 gegeben.
gegeben. |
Wie lang wird eine Strecke
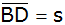 , wenn D
auf , wenn D
auf 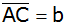 liegt und der Winkel
liegt und der Winkel
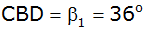 beträgt?
beträgt? |
|
2 P |
|
|
Aufgabe 8d: |
Ein Dreieck ABC ist durch die beiden Seiten
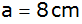 und und
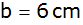 sowie
den eingeschlossenen Winkel sowie
den eingeschlossenen Winkel
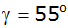 gegeben.
gegeben. |
Bestimme auch die Entfernung e des Punktes D von
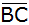 . . |
|
1 P |
|
|
Aufgabe 8e: |
Ein Dreieck ABC ist durch die beiden Seiten
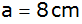 und und
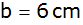 sowie
den eingeschlossenen Winkel sowie
den eingeschlossenen Winkel
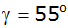 gegeben.
gegeben. |
Die Höhe  im gegebenen Dreieck ABC soll Symmetrieachse eines
gleichschenkligen Teildreiecks sein,
im gegebenen Dreieck ABC soll Symmetrieachse eines
gleichschenkligen Teildreiecks sein,
dessen Spitze in A
und dessen Grundseite auf
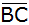 liegt.
liegt. |
Wie groß sind die Winkel und Schenkel dieses Teildreiecks,
wenn seine Grundseite d halb so lang wie
die Seite a
ist? |
|
2 P |
|