|
Aufgabe 1a: |
| Ein
Langstreckenläufer beginnt sein Training mit einer
bestimmten Anfangsstrecke und erhöht sein Laufpensum
jeden Tag um 500 m. Am 9. Tag läuft er auf diese
Weise eine doppelt so lange Strecke wie am 4. Tag.
Da er dieses tägliche Training ohne Unterbrechungen
mehrere Wochen lang fortsetzt, legt er schließlich
eine Gesamtstrecke von 247,5 km zurück. |
|
Mit welcher Strecke beginnt er sein Training? |
|
|
4 P |
|
|
Aufgabe 1b: |
| Ein
Langstreckenläufer beginnt sein Training mit einer
bestimmten Anfangsstrecke und erhöht sein Laufpensum
jeden Tag um 500 m. Am 9. Tag läuft er auf diese
Weise eine doppelt so lange Strecke wie am 4. Tag.
Da er dieses tägliche Training ohne Unterbrechungen
mehrere Wochen lang fortsetzt, legt er schließlich
eine Gesamtstrecke von 247,5 km zurück. |
|
Wieviel Tage dauert das Training? |
|
|
4 P |
|
|
Aufgabe 1c: |
| Ein
Langstreckenläufer beginnt sein Training mit einer
bestimmten Anfangsstrecke und erhöht sein Laufpensum
jeden Tag um 500 m. Am 9. Tag läuft er auf diese
Weise eine doppelt so lange Strecke wie am 4. Tag.
Da er dieses tägliche Training ohne Unterbrechungen
mehrere Wochen lang fortsetzt, legt er schließlich
eine Gesamtstrecke von 247,5 km zurück. |
|
Wie lang ist die Strecke, die er am letzten Tag
zurücklegt? |
|
|
3 P |
|
|
Aufgabe 2a: |
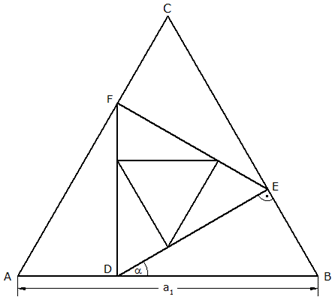
| Nebenstehende Skizze zeigt die ersten
drei Glieder einer Dreiecksfolge. Die Punkte
D, E und F teilen die Seiten des
gleichseitigen Dreiecks ABC im Verhältnis 1
: 2; die weiteren Dreiecke werden
fortlaufend in gleicher Weise
einbeschrieben. |
Das erste Dreieck hat die Seitenlänge
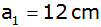 . . |
| Zeichne die ersten vier Dreiecke der
Folge! |
|
 |
|
|
4 P |
|
|
Aufgabe 2b: |
| Nebenstehende Skizze zeigt die ersten
drei Glieder einer Dreiecksfolge. Die Punkte
D, E und F teilen die Seiten des
gleichseitigen Dreiecks ABC im Verhältnis 1
: 2; die weiteren Dreiecke werden
fortlaufend in gleicher Weise
einbeschrieben. |
Das erste Dreieck hat die Seitenlänge
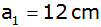 . . |
Bestimme den Winkel
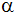 und beweise, daß das Dreieck DEF
gleichseitig ist!
und beweise, daß das Dreieck DEF
gleichseitig ist! |
|
 |
|
|
4 P |
|
|
Aufgabe 2c: |
| Nebenstehende Skizze zeigt die ersten
drei Glieder einer Dreiecksfolge. Die Punkte
D, E und F teilen die Seiten des
gleichseitigen Dreiecks ABC im Verhältnis 1
: 2; die weiteren Dreiecke werden
fortlaufend in gleicher Weise
einbeschrieben. |
Das erste Dreieck hat die Seitenlänge
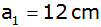 . . |
| Wie groß ist der Quotient der
Dreiecksfolge? |
|
 |
|
|
1 P |
|
|
Aufgabe 2d: |
| Nebenstehende Skizze zeigt die ersten
drei Glieder einer Dreiecksfolge. Die Punkte
D, E und F teilen die Seiten des
gleichseitigen Dreiecks ABC im Verhältnis 1
: 2; die weiteren Dreiecke werden
fortlaufend in gleicher Weise
einbeschrieben. |
Das erste Dreieck hat die Seitenlänge
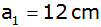 . . |
| Stelle die allgemeinen Formeln für den
n-ten Dreiecksumfang und für die n-te
Dreiecksfläche auf und berechne diese Größen
für n = 4! |
|
 |
|
|
4 P |
|
|
Aufgabe 3a: |
Eine
arithmetische Zahlenfolge besteht aus den drei
Gliedern
 ;
eine geometrische Zahlenfolge aus den drei Gliedern ;
eine geometrische Zahlenfolge aus den drei Gliedern
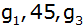 .
Anfangsglieder und Endglieder beider Zahlenfolgen
sind gleich. .
Anfangsglieder und Endglieder beider Zahlenfolgen
sind gleich. |
|
Wie heißen die Zahlenfolgen? |
|
|
4 P |
|
|
Aufgabe 3b: |
Eine
arithmetische Zahlenfolge besteht aus den drei
Gliedern
 ;
eine geometrische Zahlenfolge aus den drei Gliedern ;
eine geometrische Zahlenfolge aus den drei Gliedern
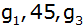 .
Anfangsglieder und Endglieder beider Zahlenfolgen
sind gleich. .
Anfangsglieder und Endglieder beider Zahlenfolgen
sind gleich. |
|
Berechne d und q der Zahlenfolgen! |
|
|
4 P |
|
|
Aufgabe 4a: |
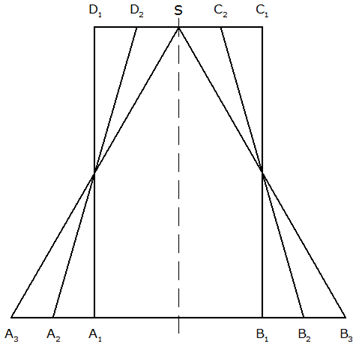
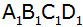 ist der Achsenschnitt eines Zylinders,
ist der Achsenschnitt eines Zylinders,
 der eines Kegelstumpfes und
der eines Kegelstumpfes und
 der eines Kegels. Diese drei Drehkörper
haben eine gemeinsame Achse und sind gleich
hoch (
der eines Kegels. Diese drei Drehkörper
haben eine gemeinsame Achse und sind gleich
hoch ( ),
ihre Achsenschnitte sind flächengleich ( ),
ihre Achsenschnitte sind flächengleich ( ).
Ferner gilt: ).
Ferner gilt:
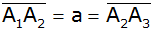 . . |
Berechne die Rauminhalte des Zylinders,
Kegelstumpfes und Kegels und die
Verhältnisse
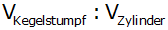 und
und
 ! ! |
|
 |
|
|
4 P |
|
|
Aufgabe 4b: |
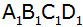 ist der Achsenschnitt eines Zylinders,
ist der Achsenschnitt eines Zylinders,
 der eines Kegelstumpfes und
der eines Kegelstumpfes und
 der eines Kegels. Diese drei Drehkörper
haben eine gemeinsame Achse und sind gleich
hoch (
der eines Kegels. Diese drei Drehkörper
haben eine gemeinsame Achse und sind gleich
hoch ( ),
ihre Achsenschnitte sind flächengleich ( ),
ihre Achsenschnitte sind flächengleich ( ).
Ferner gilt: ).
Ferner gilt:
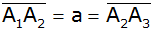 . . |
| Um welche Größe e muß man den unteren
Radius des Zylinders verlängern und den
oberen Radius verkürzen, daß bei
flächengleichem Achsenschnitt das Volumen
des entstehenden Kegelstumpfes 1,25 mal so
groß wie das Volumen des Zylinders wird? |
|
 |
|
|
4 P |
|
|
Aufgabe 4c: |
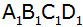 ist der Achsenschnitt eines Zylinders,
ist der Achsenschnitt eines Zylinders,
 der eines Kegelstumpfes und
der eines Kegelstumpfes und
 der eines Kegels. Diese drei Drehkörper
haben eine gemeinsame Achse und sind gleich
hoch (
der eines Kegels. Diese drei Drehkörper
haben eine gemeinsame Achse und sind gleich
hoch ( ),
ihre Achsenschnitte sind flächengleich ( ),
ihre Achsenschnitte sind flächengleich ( ).
Ferner gilt: ).
Ferner gilt:
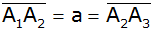 . . |
Warum ist das Ergebnis von 4b unabhängig
von der
Höhe h? |
|
 |
|
|
1 P |
|
|
Aufgabe 4d: |
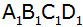 ist der Achsenschnitt eines Zylinders,
ist der Achsenschnitt eines Zylinders,
 der eines Kegelstumpfes und
der eines Kegelstumpfes und
 der eines Kegels. Diese drei Drehkörper
haben eine gemeinsame Achse und sind gleich
hoch (
der eines Kegels. Diese drei Drehkörper
haben eine gemeinsame Achse und sind gleich
hoch ( ),
ihre Achsenschnitte sind flächengleich ( ),
ihre Achsenschnitte sind flächengleich ( ).
Ferner gilt: ).
Ferner gilt:
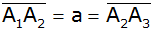 . . |
Zeichne die Achsenschnitte aller vier
Körper
im Maßstab 1 : 2 so, daß die
Achsen zusammenfallen! |
|
 |
|
|
2 P |
|
|
Aufgabe 5a: |
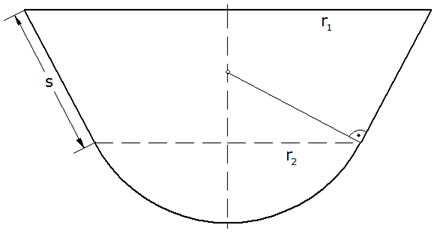
Ein Sudkessel (siehe nebenstehende
Skizze) hat die Form eines sich nach unten
verengenden Kegelstumpfes mit einem
Kugelabschnitt als Boden, der kantenlos in
den Mantel des Kegelstumpfes übergeht. Die
Maße sind:
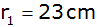 , ,
 und
und
 . . |
Berechne für den Kegelstumpf die Höhe
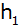 und für den Kugelabschnitt die Höhe
und für den Kugelabschnitt die Höhe
 und den Krümmungsradius r!
und den Krümmungsradius r! |
|
 |
|
|
4 P |
|
|
Aufgabe 5b: |
Ein Sudkessel (siehe nebenstehende
Skizze) hat die Form eines sich nach unten
verengenden Kegelstumpfes mit einem
Kugelabschnitt als Boden, der kantenlos in
den Mantel des Kegelstumpfes übergeht. Die
Maße sind:
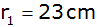 , ,
 und
und
 . . |
| Zeichne einen Achsenschnitt im Maßstab 1
: 4! |
|
 |
|
|
3 P |
|
|
Aufgabe 5c: |
Ein Sudkessel (siehe nebenstehende
Skizze) hat die Form eines sich nach unten
verengenden Kegelstumpfes mit einem
Kugelabschnitt als Boden, der kantenlos in
den Mantel des Kegelstumpfes übergeht. Die
Maße sind:
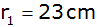 , ,
 und
und
 . . |
| Wie groß ist das Volumen des Kessels? |
|
 |
|
|
4 P |
|
|
Aufgabe 6a: |
Die untere
Grundfläche eines regelmäßigen Pyramidenstumpfes ist
ein Sechseck mit der Fläche
 .
Die Deckfläche .
Die Deckfläche
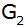 ist halb so groß wie
ist halb so groß wie
 .
Die Raumdiagonalen, die mit der Achse einen Punkt
gemeinsam haben, sind .
Die Raumdiagonalen, die mit der Achse einen Punkt
gemeinsam haben, sind
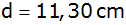 lang.
lang. |
|
Berechne das Volumen des Pyramidenstumpfes! |
|
|
4 P |
|
|
Aufgabe 6b: |
Die untere
Grundfläche eines regelmäßigen Pyramidenstumpfes ist
ein Sechseck mit der Fläche
 .
Die Deckfläche .
Die Deckfläche
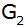 ist halb so groß wie
ist halb so groß wie
 .
Die Raumdiagonalen, die mit der Achse einen Punkt
gemeinsam haben, sind .
Die Raumdiagonalen, die mit der Achse einen Punkt
gemeinsam haben, sind
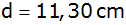 lang.
lang. |
|
Zeichne den Achsenschnitt, der vier Ecken enthält,
im Maßstab 1 : 1! |
|
|
4 P |
|
|
Aufgabe 6c: |
Die untere
Grundfläche eines regelmäßigen Pyramidenstumpfes ist
ein Sechseck mit der Fläche
 .
Die Deckfläche .
Die Deckfläche
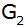 ist halb so groß wie
ist halb so groß wie
 .
Die Raumdiagonalen, die mit der Achse einen Punkt
gemeinsam haben, sind .
Die Raumdiagonalen, die mit der Achse einen Punkt
gemeinsam haben, sind
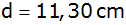 lang.
lang. |
Wie groß ist der Neigungswinkel
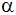 ,
unter dem die Seitenkante ,
unter dem die Seitenkante
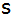 gegen die Grundfläche
gegen die Grundfläche
 geneigt ist?
geneigt ist? |
|
|
4 P |
|
|
Aufgabe 7a: |
In einem
rechtwinkligen Koordinatensystem mit der Einheit 1
cm hat ein Dreieck die Eckpunkte
 , ,
 , ,
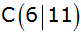 . . |
|
Zeichne dieses Dreieck im Koordinatensystem. |
|
|
1 P |
|
|
Aufgabe 7b: |
In einem
rechtwinkligen Koordinatensystem mit der Einheit 1
cm hat ein Dreieck die Eckpunkte
 , ,
 , ,
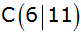 . . |
|
Berechne den Umfang des Dreiecks! |
|
|
2 P |
|
|
Aufgabe 7c: |
In einem
rechtwinkligen Koordinatensystem mit der Einheit 1
cm hat ein Dreieck die Eckpunkte
 , ,
 , ,
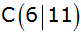 . . |
Berechne die Winkel
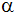 , ,
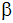 und
und
 des Dreiecks!
des Dreiecks! |
|
|
2 P |
|
|
Aufgabe 7d: |
In einem
rechtwinkligen Koordinatensystem mit der Einheit 1
cm hat ein Dreieck die Eckpunkte
 , ,
 , ,
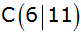 . . |
|
Berechne den Flächeninhalt des Dreiecks! |
|
|
2 P |
|
|
Aufgabe 7e: |
In einem
rechtwinkligen Koordinatensystem mit der Einheit 1
cm hat ein Dreieck die Eckpunkte
 , ,
 , ,
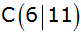 . . |
Berechne den Umkreisradius
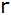 des Dreiecks und zeichne den Umkreis ein!
des Dreiecks und zeichne den Umkreis ein! |
|
|
2 P |
|
|
Aufgabe 7f: |
In einem
rechtwinkligen Koordinatensystem mit der Einheit 1
cm hat ein Dreieck die Eckpunkte
 , ,
 , ,
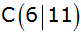 . . |
Berechne den Inkreisradius
 des Dreiecks und zeichne den Inkreis ein!
des Dreiecks und zeichne den Inkreis ein! |
|
|
2 P |
|
|
Aufgabe 8a: |
Das Teilstück
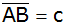 einer geplanten Straße muß gradlinig ein sumpfiges
Geländestück überqueren. Vom Punkt
einer geplanten Straße muß gradlinig ein sumpfiges
Geländestück überqueren. Vom Punkt
 aus werden folgende Vermessungen durchgeführt:
aus werden folgende Vermessungen durchgeführt:
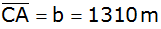 , ,
 , ,
 . . |
|
Zeichne einen Lageplan im Maßstab 1 : 10000! |
|
|
3 P |
|
|
Aufgabe 8b: |
Das Teilstück
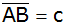 einer geplanten Straße muß gradlinig ein sumpfiges
Geländestück überqueren. Vom Punkt
einer geplanten Straße muß gradlinig ein sumpfiges
Geländestück überqueren. Vom Punkt
 aus werden folgende Vermessungen durchgeführt:
aus werden folgende Vermessungen durchgeführt:
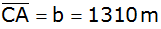 , ,
 , ,
 . . |
Berechne die Länge
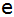 des den Sumpf überquerenden Straßenstücks, wenn es
bei dem Geländepunkt
des den Sumpf überquerenden Straßenstücks, wenn es
bei dem Geländepunkt
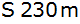 nach
nach
 beginnt und bei dem Geländepunkt
beginnt und bei dem Geländepunkt
 vor
vor
 endet!
endet! |
|
|
4 P |
|
|
Aufgabe 8c: |
Das Teilstück
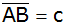 einer geplanten Straße muß gradlinig ein sumpfiges
Geländestück überqueren. Vom Punkt
einer geplanten Straße muß gradlinig ein sumpfiges
Geländestück überqueren. Vom Punkt
 aus werden folgende Vermessungen durchgeführt:
aus werden folgende Vermessungen durchgeführt:
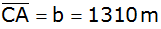 , ,
 , ,
 . . |
In einem späteren Bauabschnitt soll von Punkt
 aus eine gradlinige Verbindungsstraße nach Punkt
aus eine gradlinige Verbindungsstraße nach Punkt
 gebaut werden. Berechne die Länge
gebaut werden. Berechne die Länge
 dieser Straße!
dieser Straße! |
|
|
4 P |
|