1.
Berechnung der
Funktionsgleichung der Parabel
 : |
 |
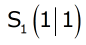Scheitelpunkt |
 |
Scheitelform |
 |
|
 |
|
 |
Allgemeine Parabelgleichung |
 |
|
|
|
 |
2.
Berechnung der Funktionsgleichung
der Parabel
 : |
|
|
Allgemeine Parabelgleichung |
|
|
 |
|
|
Punktkoordinaten einsetzen |
 |
|
 |
Seiten tauschen |
 |
 |
 |
Gleichsetzungsverfahren |
 |
 |
 |
 |
 |
p = 8 in II'' einsetzen |
 |
|
 |
|
 |
|
 |
|
|
|
 |
3. Berechnung der
Funktionsgleichung der Geraden
: |
 |
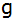Allgemeine Geradengleichung |
| |
 |
| |
Punktkoordinaten einsetzen |
 |
Seiten tauschen |
 |
 |
 |
Gleichsetzungsverfahren |
 |
 |
 |
 |
 |
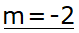m = -2 in I' einsetzen |
 |
|
|
|
|
 |
|
 |
|
|
 |
4. Berechnung der
Koordinaten von
 : |
 |
Funktionsgleichung von
 |
 |
quadratische Ergänzung |
 |
|
 |
|
|
 |
5. Berechnung der
Entfernung zwischen
und
: |
 |
Pythagoras im
gelben Dreieck |
 |
|
 |
 |
 |
|
|
 |
| 6. Behauptung
von Milo: |
Antwort:
Milo hat Recht. Die Parabeln
und
sowie die Gerade g schneiden sich im Punkt
 . |
| x |
-2 |
-1 |
0 |
1 |
2 |
3 |
| p1 |
10 |
5 |
2 |
1 |
2 |
5 |
| p2 |
0 |
5 |
12 |
21 |
|
|
| g |
7 |
5 |
3 |
1 |
-3 |
|
|
|
 |
