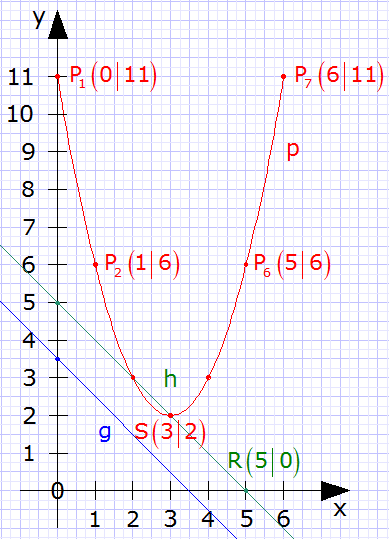
| 1. Bestimmung der
Parabelgleichung p durch Berechnung: |
 |
Allgemeine Parabelgleichung
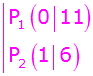
Punktkoordinaten einsetzen |
 |
|
 |
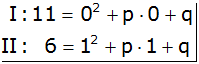Seiten
tauschen |
 |
|
 |
q = 11
in II' einsetzen |
 |
Zusammenfassen |
 |
 |
 |
|
 |
|
|
|
| |
|
|
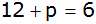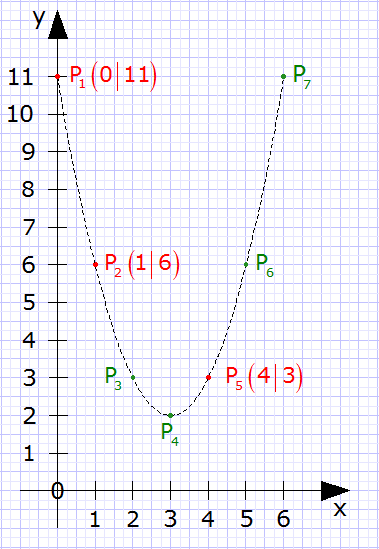
P1 |
P2 |
P3 |
P4 |
P5 |
P6 |
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
|
y |
11 |
6 |
|
|
3 |
|
|
|
 |
|
|
2. Vollständige
Wertetabelle: |
|
|
|
 |
|
3. Rechnerischer
Beweis, dass p und g keinen gemeinsamen Punkt besitzen: |
 |
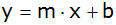Allgemeine Geradengleichung |
 |
 |
 |
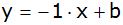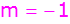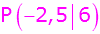Punktkoordinaten einsetzen |
 |
|
 |
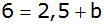Seiten
tauschen |
 |
 |
 |
|
 |
|
 |
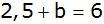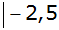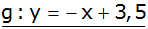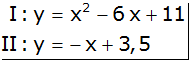Gleichsetzungsverfahren |
 |
 |
 |
 |
 |
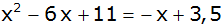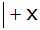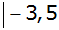Normalform einer quadratischen Gleichung |
 |
|
 |
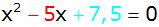p und
q bestimmen |
 |
|
 |
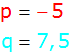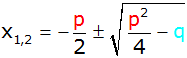Lösungsformel |
 |
|
 |
|
 |
|
 |
|
|
 |
|
 |
|
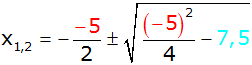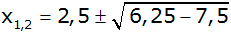4. Berechnung der
Koordinaten des Schnittpunktes R: |
|
|
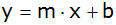Allgemeine
Geradengleichung |
 |
|
,
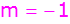da g und h parallel |
|
 |
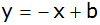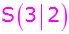Punktkoordinaten
einsetzen |
|
 |
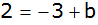Seiten tauschen |
 |
 |
 |
|
 |
|
 |
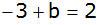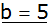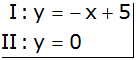Gleichsetzungsverfahren |
|
 |
 |
 |
 |
 |
|
 |
|
|
|
 |
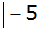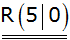