|
Wahlaufgaben |
|
Aufgabe B/4a: |
Die Parabel
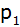 hat die
Funktionsgleichung hat die
Funktionsgleichung
 . . |
Die verschobene nach oben geöffnete Normalparabel
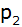 hat den
Scheitelpunkt hat den
Scheitelpunkt
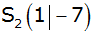 . . |
 |
Berechnen Sie die
Koordinaten des Schnittpunktes
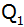 der beiden Parabeln
der beiden Parabeln
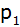 und
und
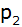 . . |
|
Die Parabel
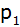 schneidet die x-Achse in den Punkten
schneidet die x-Achse in den Punkten
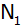 und und
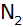 . . |
 |
Berechnen Sie die
Koordinaten von
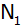 und
und
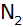 . . |
|
Die Punkte
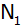 , ,
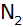 und und
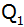 bilden
ein Dreieck. bilden
ein Dreieck. |
 |
Berechnen Sie den
Flächeninhalt des Dreiecks
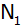 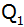 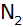 . . |
|
Der Punkt
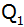 bewegt
sich auf der Parabel bewegt
sich auf der Parabel
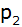 unterhalb der x-Achse.
unterhalb der x-Achse.
Dadurch entsteht der Punkt
 und
somit das Dreieck und
somit das Dreieck
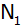  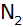 . . |
 |
Für welche Lage von
 wird der Flächeninhalt des Dreiecks am größten?
wird der Flächeninhalt des Dreiecks am größten? |
|
 |
Berechnen Sie diesen
maximalen Flächeninhalt. |
|