Die nach
oben geöffnete Normalparabel
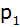hat mit der x-Achse die Schnittpunkte
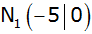und
 .
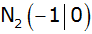Sie schneidet die y-Achse im Punkt A.
|
| |
Die Parabel
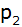hat die Funktionsgleichung
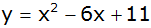und schneidet die y-Achse im Punkt B. |
| |
Durch die
Scheitelpunkte
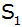und
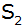der beiden Parabeln verläuft die Gerade g. Berechnen
Sie die Funktionsgleichung der Geraden g. |
| |
Der Punkt C ist
der Mittelpunkt der Strecke
 .
Die Gerade h mit der Steigung m = - 1 geht durch C.
Unter welchen Winkeln schneiden sich die Geraden g
und h?
Begründen Sie Ihre Antwort durch Rechnung
oder Argumentation. |
