Home Geschichte Informatik Lernmaterial Linkliste Mathematik Smartphone ARS LB
2023 Übersicht
nach oben
Pflichtaufgaben
Aufgabe A1/1: 1 P
In der nebenstehenden Figur fehlen die Beschriftungen zweier Punkte und zweier Winkel.
Tragen Sie die Punkte S und U sowie die Winkel und 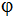in die Kästchen ein. sodass die folgende Aussagen zutreffen.		  
Aufgabe A1/2a:
Zwei Spielwürfel werden gleichzeitig geworfen.
Die Augenzahlen werden addiert (Augensumme).

Berechnen Sie die Wahrscheinlichkeit für das Ereignis "Augensumme ungerade".
1 P
Aufgabe A1/2b:
Zwei Spielwürfel werden gleichzeitig geworfen.
Die Augenzahlen werden addiert (Augensumme).

Berechnen Sie die Wahrscheinlichkeit für das Ereignis "Augensumme kleiner als 4".
1 P
Aufgabe A1/3:
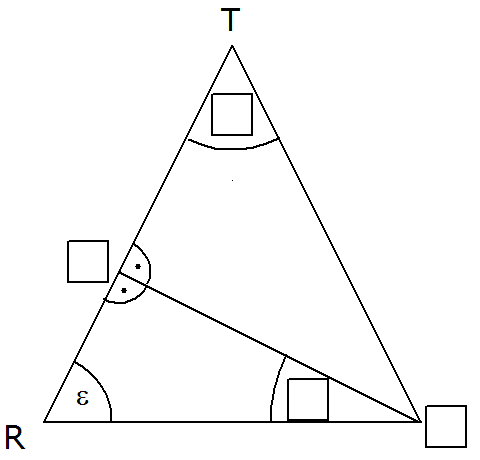
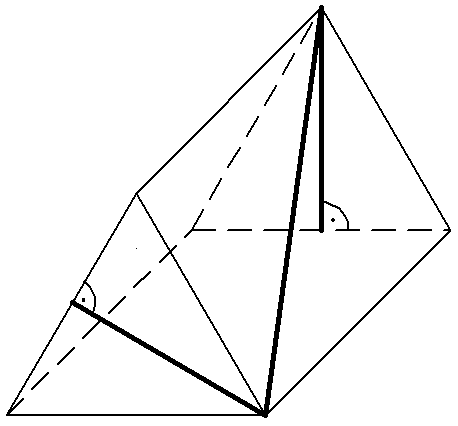
Auf der Oberfläche des Dreiecksprismas ist ein Streckenzug eingezeichnet.
Die Grund- und die Deckfläche sind gleichseitige Dreiecke.

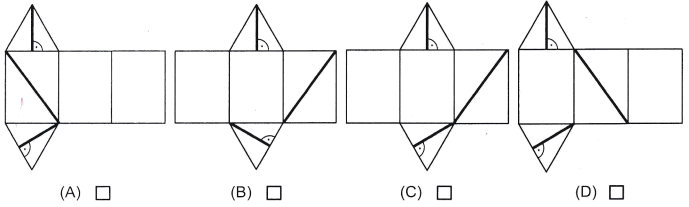
Auf welchem Netz ist der Streckenzug richtig abgebildet? Kreuzen Sie an.
1 P
Aufgabe A1/4:
Die Funktionsgleichungen von drei Parabeln sind gegeben.

      


Welche der drei Parabeln schneidet die x-Achse zweimal?
Begründen Sie Ihre Entscheidung.
  1 P
Aufgabe A1/5:
Welche Zahl muss eingesetzt werden?

         		 
  1 P
Aufgabe A1/6:
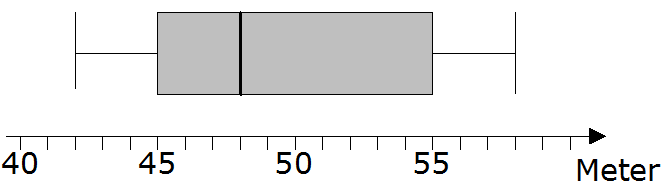
Welcher der beiden Ranglisten gehört zum abgebildeten Boxplot?
Begründen Sie mithilfe der Kennwerte.
 
 
 
 
 
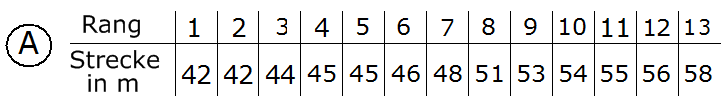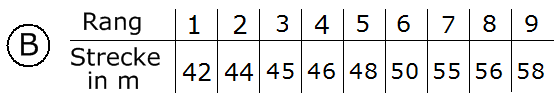1 P
Aufgabe A1/7:    
80 Jugendliche wurden befragt, welchen Freizeitsport sie betreiben. Die Ergebnisse dieser Befragung sind in der Tabelle abgebildet.
Welches der drei Diagramme gehört zur Tabelle?
Begründen Sie Ihre Entscheidung.		 1,5 P
     
Aufgabe A1/8a: 0,5 P
Emily hat vier Muster aus Plättchen gelegt.  
Wie viele Plättchen benötigt Emily für das 8. Muster?
Aufgabe A1/8b:  
Emily hat vier Muster aus Plättchen gelegt. 1 P
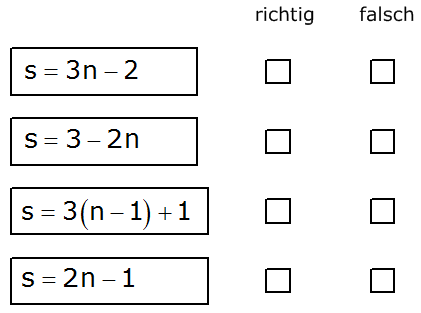
Emily möchte die Anzahl der Plättchen bei jedem Muster berechnen.
Sie hat vier Formeln zur Auswahl.
n gibt die Stelle des jeweiligen Musters an,
s ist die Summe der Plättchen eines Musters.
Welche beiden Formeln kann Emily verwenden?
Kreuzen Sie jeweils richtig oder falsch an.
                  
Aufgabe A2/1:
Im rechtwinkligen Dreieck ABC liegen die beiden gleichschenkligen Dreiecke ABD und BCD.

Es gilt:
 
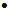Berechnen Sie den Umfang des Dreiecks ABD.
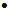Berechnen Sie den Flächeninhalt des Dreiecks ABD.
  3,5 P
Aufgabe A2/2:
Ein zusammengesetzter Körper besteht aus einem quadratischen Prisma mit aufgesetzter quadratischen Pyramide.
Dieser zusammengesetzte Körper wurde durch einen Parallelschnitt halbiert.
Die Schnittfläche 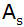ist grau eingefärbt.

Es gilt:
   
Berechnen Sie den Flächeninhalt der Schnittfläche . 
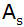  4 P
Aufgabe A2/3:

Lösen Sie das Gleichungssystem:
  3 P
Aufgabe A2/4:
Die Abbildung zeigt den Ausschnitt einer verschobenen nach oben geöffneten Normalparabel p.
Bestimmen Sie die Funktionsgleichung der Normalparabel p. Entnehmen Sie dazu geeignete Werte aus der Zeichnung.
Eine Gerade g schneidet die y-Achse im Punkt 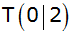und hat die Steigung .
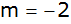  Berechnen Sie die Koordinaten der Schnittpunkte A und B der Parabel und der Geraden.
3,5 P
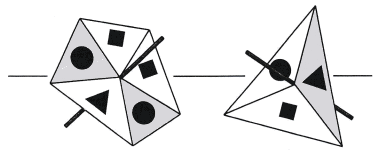
Aufgabe A2/5:
Auf zwei Kreiseln befinden sich die Symbole , und .
Die Felder eines Kreisels sind jeweils gleich groß.
Sie sind grau bzw. weiß gefärbt.
Die beiden Kreisel werden gedreht und bleiben auf einer Kante liegen.
Berechnen Sie die Wahrscheinlichkeit für folgende Ereignisse:
zwei gleiche Symbole
Kreis und Dreieck
höchsten ein graues Feld
3 P
Aufgabe A2/6:
Im Diagramm sind die Ausgaben für Onlinewerbung in Deutschland für die Jahre 2020 und 2021 dargestellt.
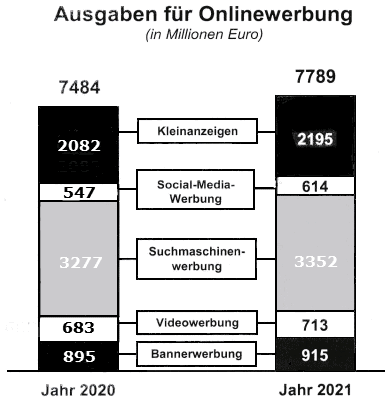Die Ausgaben für Onlinewerbung sind von 2020 bis 2021 angestiegen.
Berechnen Sie den Zuwachs in Prozent
Die Ausgaben für die Bannerwerbung lagen im Jahr 2020 um 9,5% über dem Betrag von 2019.
Berechnen Sie die Ausgaben für die Bannerwerbung im Jahr 2019.
Laut einer Prognose sollen in den fünf Jahren von 2021 bis 2026 die Ausgaben für die Social-Media-Werbung jährlich um 12,25% bezogen auf das jeweilige Vorjahr ansteigen.
Wie hoch wären die Ausgaben für die Social-Media-Werbung dann im Jahr 2026?
  3 P
Wahlaufgaben
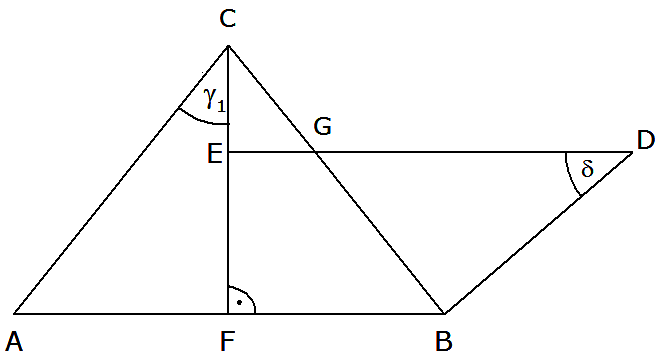
Aufgabe B/1a:
Das gleichschenklige Dreieck ABC und das rechtwinklige Trapez FBDE überdecken sich teilweise.
Es gilt:
 

Berechnen Sie den Flächeninhalt des Vierecks FBGE.
 
5 P
Aufgabe B/1b:
Eine nach oben geöffnete verschobene Normalparabel 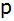mit der Form geht durch den Punkt .
  Berechnen Sie die Funktionsgleichung der Parabel .
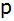Die Parabel 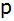geht auch durch den Punkt .
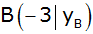Sie schneidet die y-Achse im Punkt .
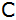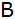  Bestimmen Sie die Koordinaten der Punkte und .
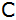Die Punkte , 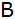und 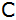bilden das Dreieck .
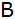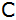  Berechnen Sie den Flächeninhalt des Dreiecks .
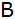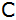Die Gerade 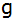geht durch den Punkt 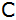und hat die Steigung .
 Geben Sie die Funktionsgleichung vo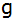n an. 
Julius behauptet: "Die Gerade 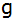halbiert den Flächeninhalt des Dreiecks ."
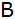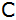 Überprüfen Sie diese Aussage und begründen Sie Ihre Antwort durch Rechnung oder Argumentation.
 
5 P
Aufgabe B/2a:
Zu einer verschobenen nach oben geöffneten Normalparabel gehört die unvollständige Wertetabelle.
     
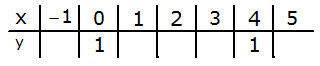  Bestimmen Sie die Funktionsgleichung von .
  Vervollständigen Sie die Wertetabelle.
Die Gerade 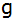hat die Funktionsgleichung und geht durch den Punkt .
 Berechnen Sie die Funktionsgleichung von . 
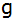Zeigen Sie rechnerisch, dass 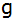keinen Schnittpunkt mit hat.
 Geben Sie die Funktionsgleichung einer verschobenen nach oben geöffneten Normalparabel 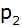an, die keinen         
  Schnittpunkt mit 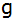und hat. 
 
5 P
Aufgabe B/2b:
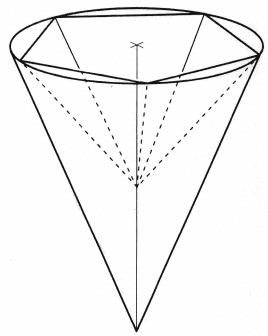
Aus einem Kegel wird eine regelmäßige fünfseitige Pyramide herausgearbeitet (siehe Abbildung).
Die Eckpunkte der Grundfläche der fünfseitigen Pyramide liegen auf der Kreislinie der Grundfläche des Kegels.

Es gilt:
 
Um wie viele cm2 unterscheiden sich die Inhalte der Mantelflächen des Kegels und der Pyramide?
5P
Aufgabe B/3a:
Die Klasse 10a verkauft Rubbellose.
Auf jedem Los befinden sich zwei Streifen.
Jeder Streifen enthält die folgenden Ziffern:
 
Die Ziffern sind in zufälliger Reihenfolge angeordnet.
Der linke Streifen zeigt die Zehnerziffern, der rechte die Einerziffern.
Auf jedem Streifen wird genau ein Feld freigerubbelt, wodurch eine zweistellige Zahl entsteht.
Die nebenstehende Abbildung zeigt die Zahl 61.
  Wie groß ist die Wahrscheinlichkeit, eine Zahl zu erhalten, die größer als 60 ist?

Die  Rubellose werden für ein Glücksspiel eingesetzt. Dazu wird nebenstehender Gewinnplan geprüft.
  Berechnen Sie den Erwartungswert. 
Die Klasse 10a überlegt, auf jedem Streifen der Lose eine  durch eine zu ersetzen.
  Erhöht sich dadurch der Gewinn für die Klasse?
Begründen Sie Ihre Entscheidung durch Rechnung.
 
5 P
Aufgabe B/3b:
Die Abbildung zeigt den Sprung eines Frosches, der annähernd die Form einer Parabel mit der Gleichung hat.
Die maximale Höhe des Sprungs ist 139 cm.
Die Sprungweite beträgt 220 cm.
  Geben Sie eine mögliche Gleichung der zugehörigen Parabel an.

In einer horizontalen Entfernung von 150 cm nach dem Absprung befindet sich ein Schilfrohr, das 94 cm aus dem Wasser ragt.
  In welchem Abstand springt der Frosch darüber?
Der Sprung eines zweiten Frosches kann mit der Gleichung dargestellt werden.
  Welcher der beiden Frösche springt weiter?
Berechnen Sie die Differenz der Sprungweiten.
 
5 P
Aufgabe B/4a:
Das Schaubild zeigt Ausschnitte der Parabel und der Geraden .
Bestimmen Sie die Funktionsgleichung von und .
Entnehmen Sie dazu geeignete Werte aus dem Schaubild.

Die Parabel schneidet die x-Achse in den Punkten und .
Geben Sie die Koordinaten von an.
Die Parabel hat die Funktionsgleichung .
Berechnen Sie die Koordinaten des Scheitelpunktes von .
 bildet mit und das Dreieck . Ebenso bildet mit und das Dreieck . 
  Um wie viele Flächeneinheiten (FE) unterscheiden sich die Flächeninhalte dieser beiden Dreiecke?
 
5 P
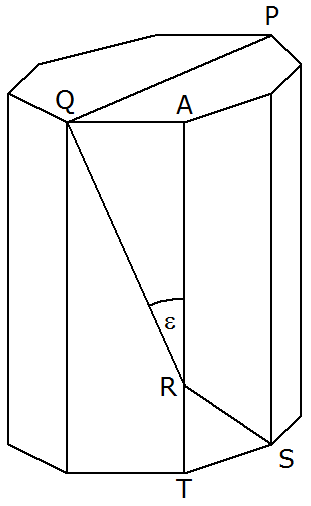
Aufgabe B/4b:
Auf einem regelmäßigen achtseitigen Prisma liegt der Streckenzug 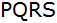mit der Länge 38,0 cm.
Es gilt:
 

Berechnen Sie die Höhe des achtseitigen Prismas.
 
5 P