|
|
| Vervollständigen Sie die Gleichung. |
|
|
|
|
|
|
|
|
Aufgabe A1/2a: |
Eine quadratische Pyramide
mit der Grundkante
 und der Körperhöhe
und der Körperhöhe
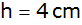 wird vollständig mit Wasser gefüllt.
wird vollständig mit Wasser gefüllt. |
| Berechnen Sie das Volumen
der Wassermenge. |
|
|
|
|
|
Aufgabe A1/2b: |
Eine quadratische Pyramide
mit der Grundkante
 und der Körperhöhe
und der Körperhöhe
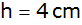 wird vollständig mit Wasser gefüllt.
wird vollständig mit Wasser gefüllt. |
Die Wassermenge wird in ein
quadratisches Prisma umgefüllt.
Die Grundkante
des quadratischen Prismas beträgt 4 cm.
Wie hoch
steht das Wasser im Prisma? |
|
|
|
|
|
Aufgabe
A1/3a: |
Ein Glücksrad mit vier gleich großen Feldern ist
weiß, schwarz und grau gefärbt.
Es wird zweimal
nacheinander gedreht.
Berechnen Sie die
Wahrscheinlichkeit des Ereignisses P(zweimal weiß). |
 |
|
|
|
|
|
Aufgabe
A1/3b: |
Ein Glücksrad mit vier gleich großen Feldern ist
weiß, schwarz und grau gefärbt.
Es wird zweimal
nacheinander gedreht.
Berechnen Sie die
Wahrscheinlichkeit des Ereignisses P(grau und
schwarz). |
 |
|
|
|
|
|
Aufgabe A1/4: |
Welcher der drei Boxplots gehört zur abgebildeten
Rangliste?
Begründen Sie mithilfe der Kennwerte. |
|
|
 |
|
|
 |
|
|
|
1,5 P
|
|
|
Aufgabe A1/5: |
|
Berechnen Sie den Term. |
|
|
|
Kreuzen Sie das zum Ergebnis zugehörige Zahlwort an. |
|
|
 |
1 Million |
|
 |
10 Millionen |
 |
1 Milliarde |
|
|
|
|
1,5 P
|
|
|
|
Emma legt Muster aus Kärtchen.
Die ersten drei Muster hat
sie bereits gelegt. |
|
|
|
Geben Sie die Anzahl der Kärtchen für das 7. Muster an
(n=7). |
|
|
|
|
|
Emma legt Muster aus Kärtchen.
Die ersten drei Muster hat
sie bereits gelegt. |
|
|
|
Eine der folgenden Formeln kann zur Berechnung der Anzahl
der Kärtchen bei allen Mustern verwendet werden. |
|
Welche Formel sollte Emma auswählen? |
 |
→ |
n gibt die Stelle des jeweiligen Musters an |
| → |
s ist die Summe der
einzelnen Kärtchen |
|
|
|
|
|
|
|
Ein Paar Sportschuhe kostet 120 €. |
|
Im Rahmen einer Rabattaktion wird der Preis um 30%
reduziert. |
|
Anschließend wird der reduzierte
Preis nochmals um 20% gesenkt. |
|
Liam behauptet: "Die Sportschuhe kosten somit nur noch die
Hälfte des ursprünglichen Preises." |
|
Hat Liam Recht? |
|
Begründen Sie Ihre Entscheidung durch Rechnung oder
Argumentation. |
|
|
|
|
Pflichtaufgaben |
|
Aufgabe A2/1: |
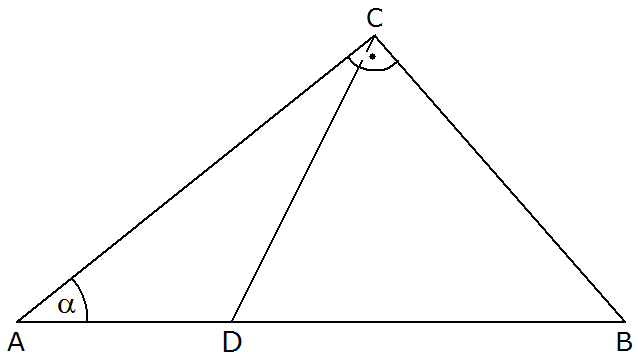
| Im rechtwinkligen Dreieck ABC gilt: |
|
|
| Berechnen Sie den Umfang des
Dreiecks ADC. |
|
 |
4 P |
|
|
Aufgabe A2/2: |
1000 Wachskugeln werden
eingeschmolzen. Sie haben jeweils einen Radius von 1,5 cm.
Mit diesem eingeschmolzenen Wachs werden quadratische
Pyramiden gegossen.
Dazu wird die abgebildete Gussform
verwendet. Diese wird vollständig mit Wachs gefüllt.
Es gilt: |
|
|
| Wie viele solcher Pyramiden können
mit dem eingeschmolzenen Wachs gegossen werden? |
|
 |
3,5 P |
|
|
|
|
Aufgabe A2/4: |
| Das Schaubild
zeigt den Ausschnitt einer verschobenen Normalparabel
p. |
|
|
|
 |
3,5 P |
Die Gerade g mit der Funktionsgleichung  schneidet die Parabel
p in den Punkten A und B. schneidet die Parabel
p in den Punkten A und B. |
|
 |
Berechnen Sie die Koordinaten der
Schnittpunkt A und B. |
|
|
|
|
Aufgabe A2/5: |
| Die Klasse 5c
verkauft Lose beim Schulfest. |
| Es gibt
folgende Gewinne: 12 Fußbälle und 8 Basketbälle. |
Die
restlichen 80 Lose sind Nieten.
|
Francesca
möchte zwei Lose ziehen.
|
|
Wie groß ist die Wahrscheinlichkeit, dass sie
|
 |
zwei Nieten zieht? |
|
 |
einen Fußball und einen Basketball
gewinnt? |
|
|
|
3 P |
|
|
Aufgabe A2/6: |
| Die
Paketzustellungen in Deutschland haben in den
letzten Jahren zugenommen. |
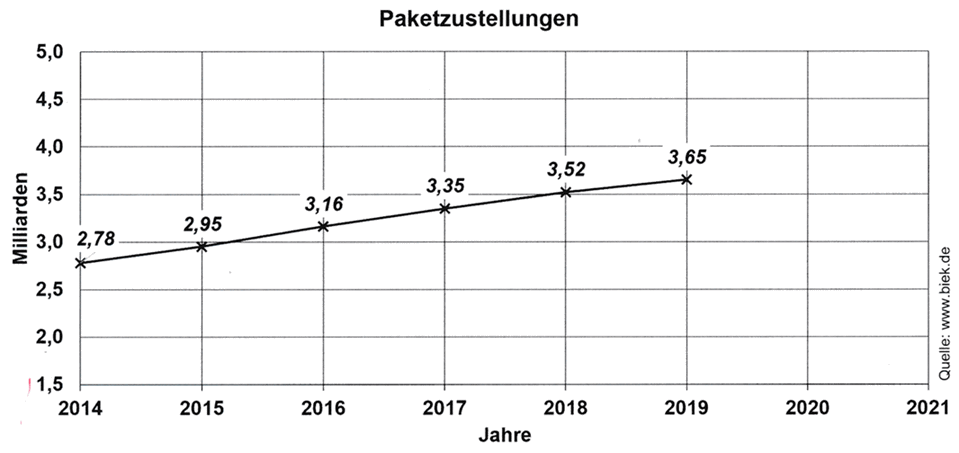
| Im Schaubild
ist diese Entwicklung dargestellt. |
|
 |
Um wie viel Prozent haben die
Paketzustellungen von 2014 bis 2019
insgesamt zugenommen? |
Der Dienstleister DHL
hatte im Jahr 2019 einen Anteil von 57,0% an
den gesamten Zustellungen. |
|
 |
Wie viele Pakete wurden von DHL im Jahr
2019 zugestellt? |
Im Jahr 2020 nahm die
Anzahl der Paketzustellungen um 9,7% zu.
Im darauffolgenden Jahr 2021 stieg die
Anzahl der Paketzustellungen um 12,5%. |
 |
Tragen Sie die Werte für 2020 und 2021
in das oben abgebildete Diagramm ein. |
|
|
|
3 P |
|
|
Wahlaufgaben |
|
Aufgabe B/1a: |
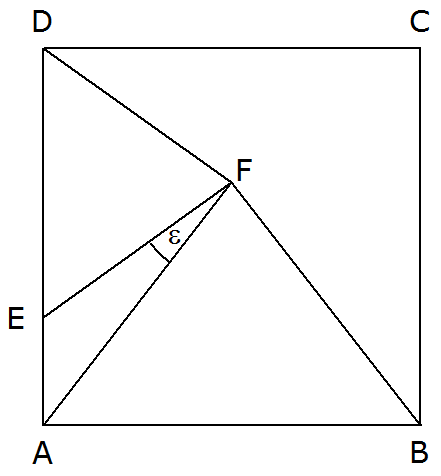
| Im Quadrat ABCD liegen die beiden
gleichschenkligen Dreiecke ABF und DEF. |
| Es gilt: |
|
|
- Berechnen Sie den Flächeninhalt des Dreiecks AFE.
|
- Berechnen Sie den Winkel
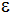 . .
|
|
 |
|
|
|
Aufgabe B/1b: |
Die Gerade
 hat die Funktionsgleichung
hat die Funktionsgleichung
 . . |
Die Parabel
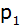 hat die Funktionsgleichung
hat die Funktionsgleichung
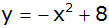 . . |
Die Parabel
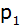 schneidet die Gerade
schneidet die Gerade
 in den Punkten
in den Punkten
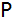 und
und
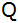 . . |
 Berechnen Sie die Koordinaten der Schnittpunkte
Berechnen Sie die Koordinaten der Schnittpunkte
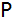 und
und
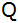 . . |
Durch die beiden
Schnittpunkte
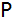 und
und
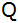 verläuft die verschobene nach oben geöffnete
Normalparabel
verläuft die verschobene nach oben geöffnete
Normalparabel
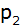 . . |
 Berechnen Sie die Koordinaten des Scheitelpunktes
Berechnen Sie die Koordinaten des Scheitelpunktes
 von
von
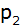 . . |
Robin behauptet: "Das
Dreieck mit den Punkten
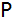 , ,
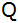 und
und
 ist rechtwinklig."
ist rechtwinklig." |
 Hat Robin Recht? Begründen Sie Ihre Antwort
rechnerisch.
Hat Robin Recht? Begründen Sie Ihre Antwort
rechnerisch. |
|
|
|
|
|
Aufgabe B/2a: |
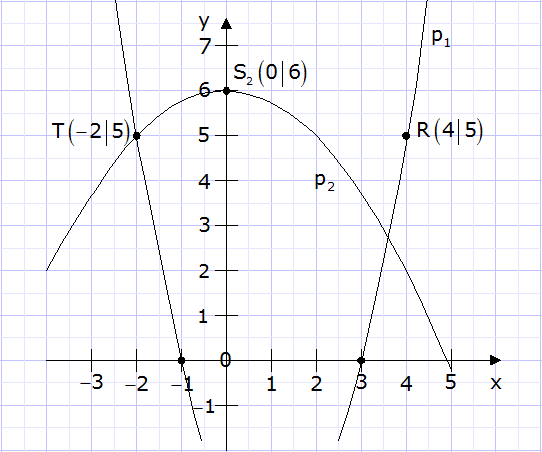
Das Schaubild zeigt Ausschnitte
der verschobenen Normalparabel
 und der
nach unten geöffneten Parabel und der
nach unten geöffneten Parabel
 . . |
- Bestimmen Sie die Funktionsgleich- ungen der beiden
Parabeln. Entnehmen Sie dazu geeignete Werte aus dem
Schaubild.
|
Die Gerade
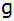 verläuft durch die beiden Scheitelpunkte
verläuft durch die beiden Scheitelpunkte
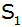 und und
 . . |
- Berechnen Sie die Funktionsgleichung von
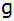 . .
|
Die Gerade
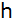 verläuft senkrecht zu
verläuft senkrecht zu
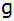 und
geht durch den Punkt und
geht durch den Punkt
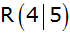 . . |
- Berechnen Sie die Funktionsgleichung von
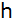 . .
|
- Geben Sie die Funktionsgleichung einer weiteren
verschobenen nach oben geöffneten Normalparabel
 an,
die keine Punkte mit an,
die keine Punkte mit
 und und
 gemeinsam hat.
gemeinsam hat.
|
|
 |
|
|
|
Aufgabe B/2b: |
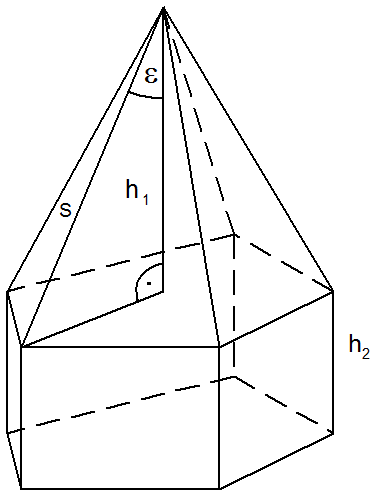
| Ein zusammengesetzter Körper besteht
aus einem regelmäßigen Fünfecksprisma mit aufgesetzter
regelmäßiger fünfseitiger Pyramide. |
| Es gilt: |
|
|
|
Berechnen Sie den Oberflächeninhalt des zusammengesetzten
Körpers.
|
|
 |
|
|
|
|
|
|
|
Aufgabe B/4a: |
Die Parabel
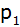 hat die
Funktionsgleichung hat die
Funktionsgleichung
 . . |
Die verschobene nach oben geöffnete Normalparabel
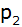 hat den
Scheitelpunkt hat den
Scheitelpunkt
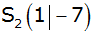 . . |
 |
Berechnen Sie die
Koordinaten des Schnittpunktes
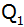 der beiden Parabeln
der beiden Parabeln
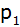 und
und
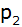 . . |
|
Die Parabel
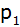 schneidet die x-Achse in den Punkten
schneidet die x-Achse in den Punkten
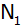 und und
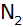 . . |
 |
Berechnen Sie die
Koordinaten von
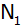 und
und
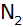 . . |
|
Die Punkte
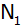 , ,
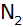 und und
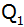 bilden
ein Dreieck. bilden
ein Dreieck. |
 |
Berechnen Sie den
Flächeninhalt des Dreiecks
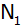 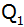 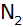 . . |
|
Der Punkt
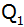 bewegt
sich auf der Parabel bewegt
sich auf der Parabel
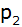 unterhalb der x-Achse.
unterhalb der x-Achse.
Dadurch entsteht der Punkt
 und
somit das Dreieck und
somit das Dreieck
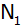  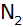 . . |
 |
Für welche Lage von
 wird der Flächeninhalt des Dreiecks am größten?
wird der Flächeninhalt des Dreiecks am größten? |
|
 |
Berechnen Sie diesen
maximalen Flächeninhalt. |
|
|
|
5 P |
|
|
Aufgabe B/4b: |
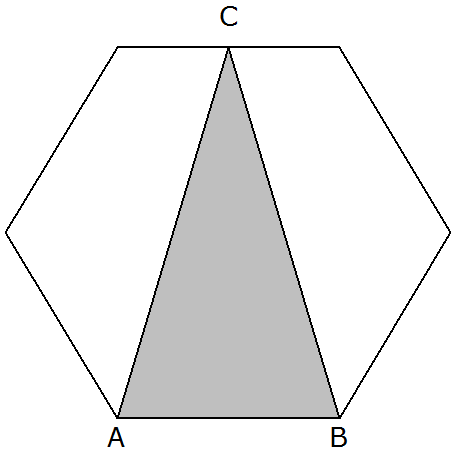
Das regelmäßige Sechseck und das
gleichschenklige Dreieck ABC haben die Seite
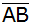 gemeinsam.
gemeinsam. |
|
Es gilt: |
|
|
 |
Berechnen Sie den Umfang des Dreiecks ABC. |
|
|
Tom behauptet: "Der Flächeninhalt des Sechsecks ist dreimal
so groß wie der Flächeninhalt des Dreiecks ABC". |
 |
Hat Tom Recht?
Begründen Sie Ihre Antwort durch
Rechnung oder Argumentation. |
|
|
 |
|
|