|
Pflichtaufgaben |
|
Aufgabe P1: |
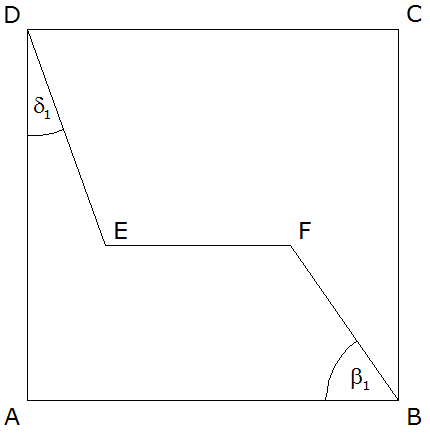
| Im Quadrat ABCD liegt der
Streckenzug DEFB. |
| Es gilt: |
|
|
Berechnen Sie den Winkel
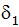 . . |
|
 |
4 P |
|
|
Aufgabe P2: |
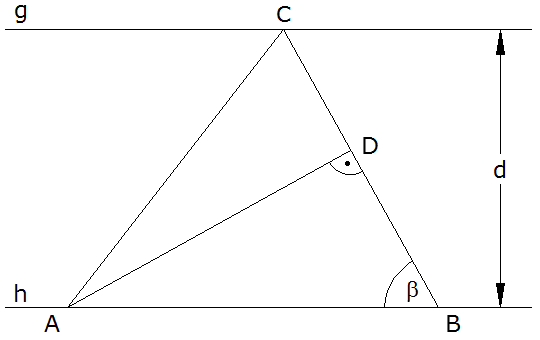
Die Eckpunkte des Dreiecks ABC
liegen auf den Parallelen g und h.
Es gilt: |
|
|
| Berechnen Sie den Umfang des
Dreiecks ADC. |
|
 |
4,5 P |
|
|
Aufgabe P3: |
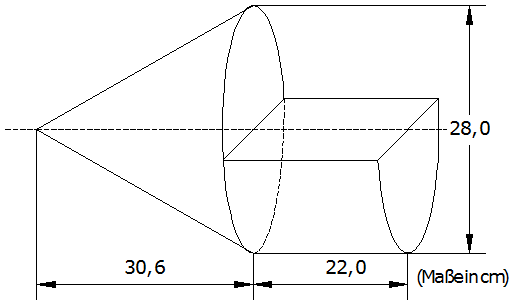
| Ein Werkstück besteht aus einem
Kegel und einem halben Zylinder. |
|
|
| Berechnen Sie den Oberflächeninhalt
des Werkstücks. |
|
 |
3,5 P |
|
|
|
|
Aufgabe P5: |
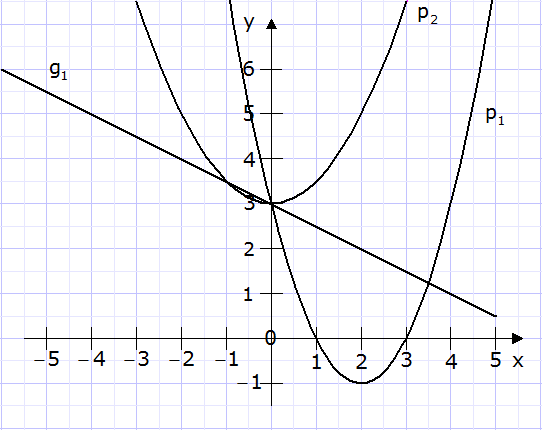
| Gegeben sind
fünf Funktionsgleichungen und drei Graphen. |
| |
 |
|
|
|
Ordnen Sie jedem Graphen die zugehörige
Funktionsgleichung zu. |
|
Begründen Sie Ihre Entscheidung. |
|
Zeichnen Sie die beiden fehlenden Graphen in das
Koordinatensystem ein. |
|
|
 |
4 P |
|
|
Aufgabe P6: |
| Ben,
Laura und Emma besitzen jeweils ein Rubbel-Los. |
| Auf
jedem Los befinden sich 16 gleich große Felder. |
| Nur
zwei der 16 Felder werden freigerubbelt. Die beiden
Beträge, die dadurch sichtbar werden, werden addiert
und ergeben den Gewinn. |
| Auf
acht Feldern steht der Betrag 0 €, auf sechs Feldern
steht der Betrag 1 € und auf zwei Feldern der Betrag
10 €. |
- Ben hat auf seinem Los zwei Felder
freigerubbelt (siehe Abbildung). Berechnen Sie
die Wahrscheinlichkeit für das Ereignis "Gewinn
10 €".
- Laura überlegt sich, wie groß die
Wahrscheinlichkeit ist, den Hauptgewinn von 20 €
zu erhalten. Berechnen Sie die
Wahrscheinlichkeit.
- Emma möchte mehr als 10 € gewinnen.
Berechnen Sie diese Wahrscheinlichkeit.
|
|
 |
|
|
4 P |
|
|
Aufgabe P7: |
| Die Diagramme zeigen
den Verbrauch von Getränkeverpackungen. |
|
|
Um wie viel Prozent ist
der Verbrauch der Einweg-Getränkeverpackungen von 2004 bis
2014
insgesamt gestiegen?
|
Wie viele Tonnen
Getränkeverpackungen (Einweg und Mehrweg) wurden im Jahr
2014 insgesamt
verbraucht?
|
Der Verbrauch von
Einweg-Getränkeverpackungen soll in zehn Jahren von 2014 bis
2024 jährlich
um jeweils 5% gegenüber dem Vorjahr
sinken.
Wie viele Tonnen Einweg-Getränkeverpackungen
wären es dann im Jahr 2024? |
|
|
3 P |
|
|
|
|
Wahlaufgaben |
|
Aufgabe W1a: |
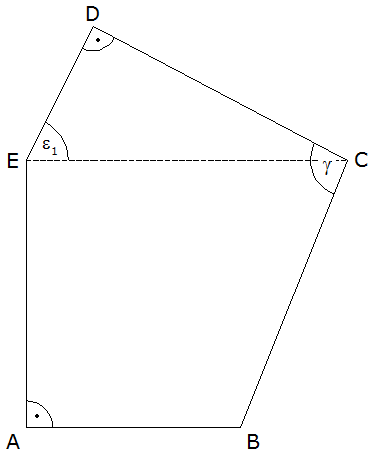
| Im Fünfeck ABCDE gilt: |
| |
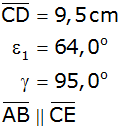 |
| |
Der Abstand des Punktes D
zu
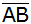 beträgt 12,9 cm.
beträgt 12,9 cm. |
|
| Berechnen Sie den Flächeninhalt des
Vierecks ABCE. |
|
 |
5,5 P |
|
|
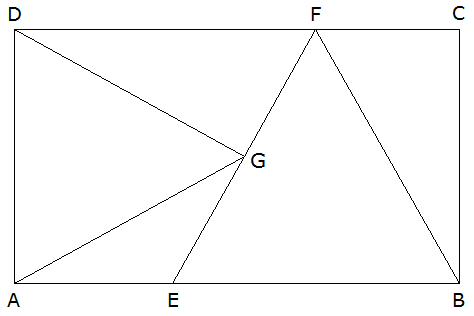
Aufgabe W1b: |
Im Rechteck ABCD liegen die
gleichseitigen Dreiecke EBF und AGD.
Es gilt: |
|
|
Weisen Sie ohne Verwendung
gerundeter Werte nach, dass für den Flächeninhalt des
Rechtecks ABCD gilt:
|
|
|
|
 |
4,5 P |
|
|
Aufgabe W2a: |
Von einer regelmäßigen achtseitigen Pyramide sind
bekannt:
|
|
|
|
|
|
Der Punkt C liegt auf der Höhe h der Pyramide. |
Das Dreieck ABC soll den gleichen Flächeninhalt
haben wie eines der Manteldreiecke.
|
Berechnen Sie die Länge von
 . . |
|
|
 |
5,5 P |
|
|
Aufgabe W2b: |
4,5 P |
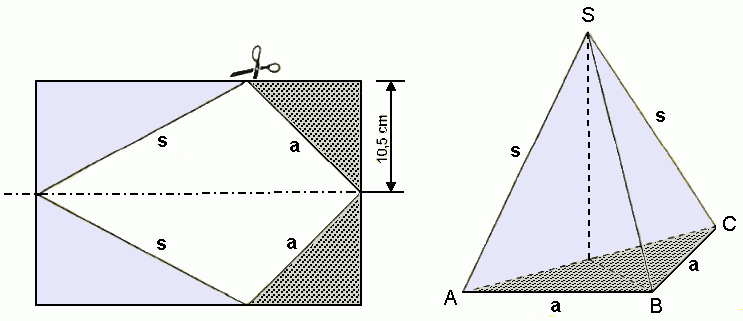
Von einem DIN-A4-Blatt (21,0 cm x 29,7 cm) werden die vier
eingefärbten Dreiecke abgeschnitten.
Mit diesen vier Dreiecken
werden die Diagonalschnittfläche ACS und die Grundfläche einer
halben
massiven quadratischen Pyramide vollständig beklebt. |
|
 |
|
|
|
|
Lena behauptet: "Die beiden Manteldreiecke ABS und BCS haben
zusammen den gleichen Flächeninhalt
wie die Restfläche des
DIN-A4-Blatts." |
|
|
|
|
|
Hat Lena Recht? Begründen Sie durch Rechnung. |
|
|
|
Aufgabe W3a: |
Die nach
oben geöffnete Normalparabel
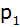 hat mit der x-Achse die Schnittpunkte
hat mit der x-Achse die Schnittpunkte
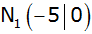 und
und
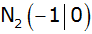 . .
Sie schneidet die y-Achse im Punkt A.
|
| |
Die Parabel
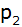 hat die Funktionsgleichung
hat die Funktionsgleichung
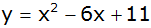 und schneidet die y-Achse im Punkt B.
und schneidet die y-Achse im Punkt B. |
| |
Durch die
Scheitelpunkte
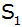 und
und
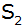 der beiden Parabeln verläuft die Gerade g. Berechnen
Sie die Funktionsgleichung der Geraden g.
der beiden Parabeln verläuft die Gerade g. Berechnen
Sie die Funktionsgleichung der Geraden g. |
| |
Der Punkt C ist
der Mittelpunkt der Strecke
 . .
Die Gerade h mit der Steigung m = - 1 geht durch C.
Unter welchen Winkeln schneiden sich die Geraden g
und h?
Begründen Sie Ihre Antwort durch Rechnung
oder Argumentation. |
|
|
|
5,5 P |
|
|
Aufgabe W3b: |
Die
Parabel
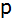 mit der Funktionsgleichung
mit der Funktionsgleichung
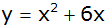 schneidet die x-Achse in den Punkten
schneidet die x-Achse in den Punkten
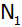 und
und
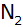 . .
|
Die Gerade
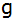 mit der Funktionsgleichung
mit der Funktionsgleichung
 schneidet die Parabel in den Punkten
schneidet die Parabel in den Punkten
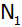 und
und
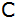 . . |
Berechnen Sie
den Flächeninhalt des Dreiecks
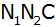 . . |
| |
Die Gerade
 mit der Funktionsgleichung
mit der Funktionsgleichung
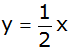 schneidet die Parabel in den Punkten
schneidet die Parabel in den Punkten
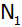 und
und
 . . |
| |
Peter
behauptet: "Die Steigung der Geraden
 ist nur halb so groß wie die der Geraden
ist nur halb so groß wie die der Geraden
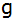 .
Daher ist der .
Daher ist der
Flächeninhalt des Dreiecks
 auch nur halb so groß wie der des Dreiecks
auch nur halb so groß wie der des Dreiecks
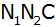 ." ." |
| Hat Peter
Recht? Begründen Sie rechnerisch. |
|
|
|
4,5 P |
|
|
Aufgabe W4a: |
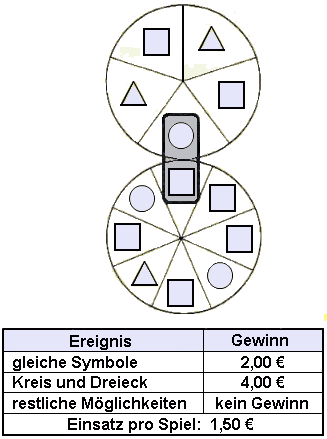
| Die beiden Glücksräder werden
gedreht. Nachdem sie stehen bleiben, erkennt man im
Sichtfenster eine Kombination zweier Symbole.
Wie groß ist die Wahrscheinlichkeit, zwei gleiche Symbole im
Sichtfenster zu sehen?
Die Glücksräder werden für ein Glücksspiel eingesetzt.
Dazu wird der abgebildete Gewinnplan geprüft.
Berechnen
Sie den Erwartungswert.
Der Gewinnplan soll so verändert werden, dass das Spiel
fair wird.
Wie hoch muss dann der Gewinn für das
Ereignis "Kreis und Dreieck" sein, wenn alles andere
unverändert bleibt?
|
|
 |
5,5 P |
|
Aufgabe W4b:
Thea trainiert Aufschläge beim
Volleyball (siehe Skizze

|
|
4,5 P |
Die Flugkurve des
Balles lässt sich mit einer Funktionsgleichung der Form
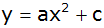 annähernd
beschreiben. Der Ball verlässt beim Aufschlag von unten die Hand in
einer Höhe von 90 cm über der Grundlinie. Nach 7,8 m (horizontal
gemessen) erreicht die Flugkurve des Balles ihre maximale Höhe von
4,0 m. annähernd
beschreiben. Der Ball verlässt beim Aufschlag von unten die Hand in
einer Höhe von 90 cm über der Grundlinie. Nach 7,8 m (horizontal
gemessen) erreicht die Flugkurve des Balles ihre maximale Höhe von
4,0 m. |
|
|
| Geben Sie eine
mögliche Funktionsgleichung der zugehörigen Parabel p an. |
|
|
| In welchem Abstand
überquert der Ball das 2,24 m hohe Netz? |
|
|
| Die Grundlinie des
Volleyballspielfeldes sind jeweils 9,0 m vom Netz entfernt (siehe
Skizze). |
|
|
| In welcher Entfernung
zur Grundlinie trifft der Ball auf dem Boden auf? |
|
|
|