|
|
|
|
|
|
|
|
2018 Übersicht
|
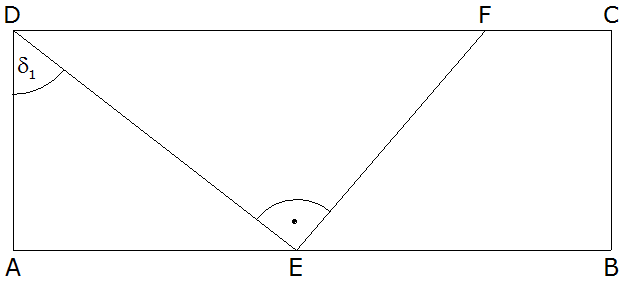 |
4 P |
|
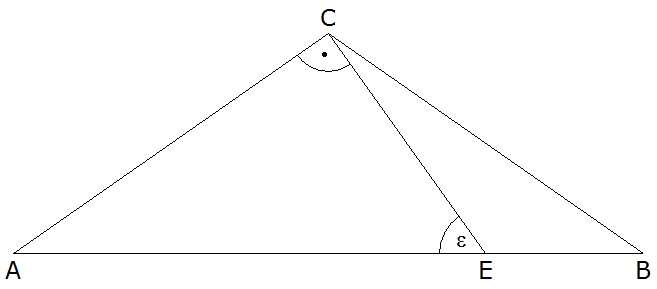 |
4 P |
|
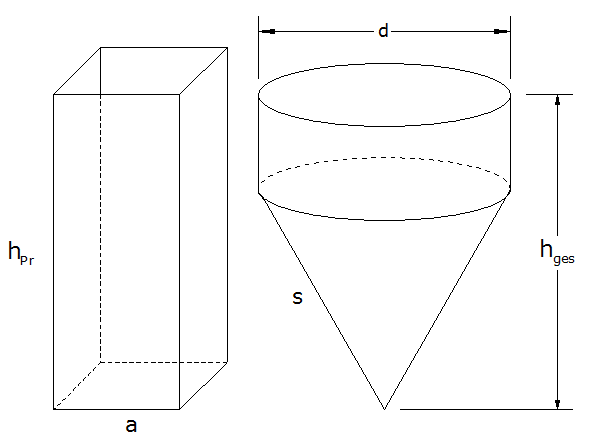 |
4 P |
|
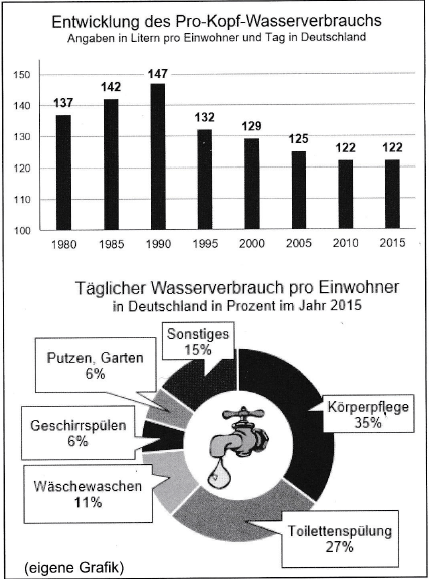 |
3,5 P |
|
3,5 P |
|
4 P |
|
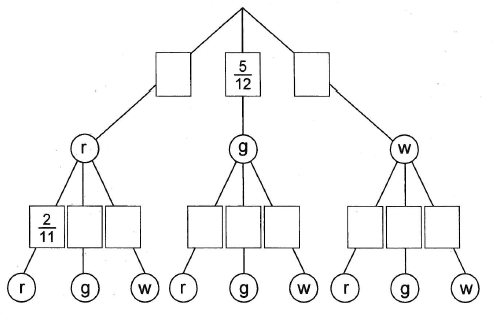 |
3,5 P |
|
3,5 P |
|
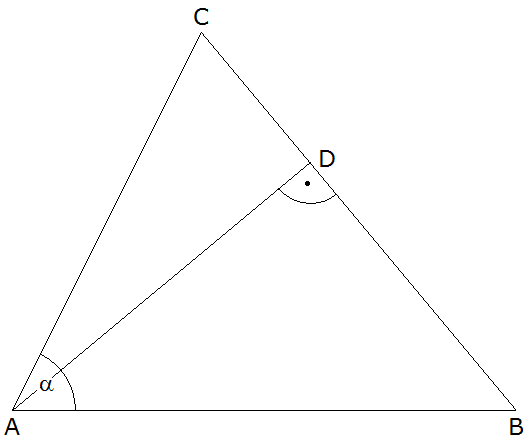 |
5,5 P | |||||||||
|
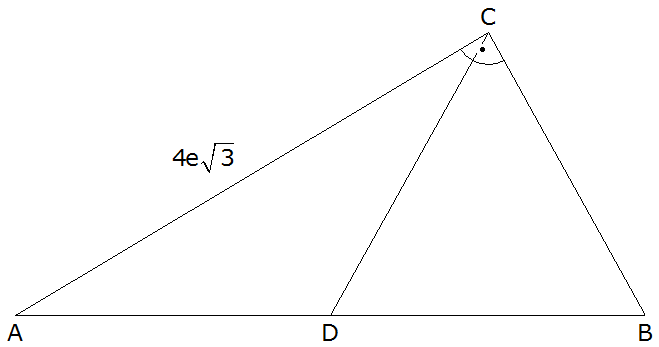 |
4,5 P |
|
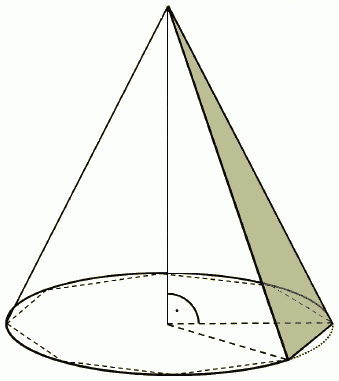 |
5 P | ||||||||
|
 |
5 P |
|
 |
5,5 P |
|
4,5 P |
|
 |
5,5 P |
|
Aufgabe W4b: Ein Golfspieler schlägt seinen Golfball ab. Die Flugbahn des Golfballes ist annähernd parabelförmig. In einer horizontalen Entfernung von 95 m zum Abschlag erreicht der Ball seine maximale Flughöhe von 25 m über dem Boden. Geben Sie eine Gleichung der zugehörigen Parabel an. Ein 15 m hoher Baum steht in 45 m Entfernung vom Abschlag. Das Loch befindet sich auf einer 2 m höher gelegenen Ebene in 180
m horizontaler Entfernung vom Abschlag. |
4,5 P |