Home Geschichte Informatik Lernmaterial Linkliste Mathematik Smartphone ARS LB
2012 Übersicht
nach oben
Pflichtaufgaben
Aufgabe P1:
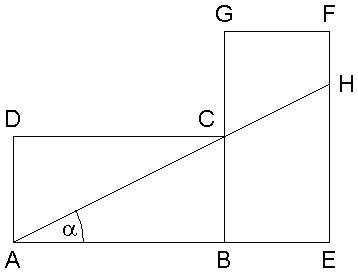
Die Rechtecke ABCD und BEFG sind kongruent.
Sie haben die Punkte B und C gemeinsam,
wobei C auf der Strecke liegt.

Es gilt:
Berechnen Sie den Flächeninhalt des Vierecks CHFG.
  4 P
Aufgabe P2:
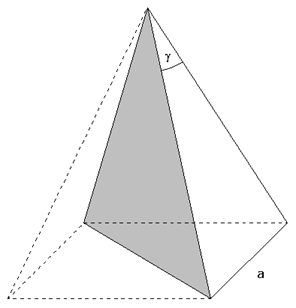
Eine massive quadratische Pyramide
wird durch einen Diagonalschnitt halbiert.

Es gilt:
Berechnen Sie die Oberfläche einer der beiden Pyramidenhälften.
4 P
Aufgabe P3:
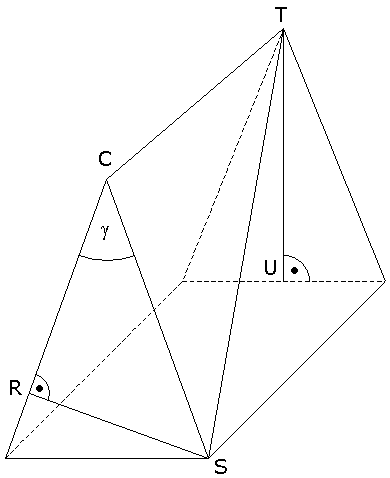
Auf einem gleichschenkligen Dreiecksprisma
liegt der Streckenzug RSTU mit der
Länge 23,4 cm.

Es gilt:
Berechnen Sie das Volumen des Prismas.
4,5 P
Aufgabe P4:
Seit dem Jahr 2007 können Städte und Kommunen Umweltzonen zur Reduzierung des Schadstoffausstoßes durch Fahrzeuge einrichten. Zur Kennzeichnung werden grüne, gelbe und rote Plaketten verwendet.

In einem Parkhaus stehen 51 Autos mit einer grünen, 23 Autos mit einer gelben und 11 Autos mit einer roten Umweltplakette.
An der Ausfahrt fahren zwei Autos nacheinander aus.

Mit welcher Wahrscheinlichkeit haben die beiden ausfahrenden Autos Plaketten mit der gleichen Farbe?

Wie groß ist die Wahrscheinlichkeit, dass mindestens eines der beiden ausfahrenden Autos eine grüne Plakette hat?
3,5 P
Aufgabe P5:

Lösen Sie das Gleichungssystem:
3 P
Aufgabe P6:
Das Schaubild zeigt einen Ausschnitt einer verschobenen Normalparabel p.
Sie schneidet die x-Achse in und .

Bestimmen Sie die Koordinaten von rechnerisch oder über eine Argumentation.

Eine Gerade g verläuft durch die Punkte und .

Berechnen Sie die Koordinaten des zweiten Schnittpunktes Q von p und g.
4 P
Aufgabe P7:
Bei einer Umfrage in der Klasse 9a der Pestalozzi-Realschule wurden 21 Schülerinnen und Schüler über die Höhe ihres monatlichen Taschengeldes befragt.
Stellen Sie die Verteilung der Daten in einem Boxplot dar.
Geben Sie die dafür notwendigen Kennwerte an.
Vier weitere Schülerinnen und Schüler der 9a wurden nachträglich befragt.
Sie erhalten folgende Taschengeldbeträge:
10 €, 20 €, 30 € und 40 €.
Verändert sich dadurch der Boxplot?
Begründen Sie Ihre Aussage.
4 P
Aufgabe P8:   3 P 
 


Das Diagramm zeigt den Energieverbrauch in Deutschland im Jahr 2010.

Dabei unterscheidet man zwischen fossilen Energieträgern und erneuerbaren Energien. Der Anteil der erneuerbaren Energien (EE) ist zusätzlich in unterschiedliche Energiearten aufgeteilt.
Petajoule (PJ) ist eine Maßeinheit für Energie.

Berechnen Sie die im Jahr 2010 durch Windenergie erzeugte Energiemenge in Petajoule (PJ).

Wie hoch ist der prozentuale Anteil der Biomasse an den erneuerbaren Energien?

 

Pauline möchte die einzelnen Energiearten der erneuerbaren Energien (Wasserkraft, Windenergie, Biomasse und restliche EE) im obigen Kreisdiagramm darstellen.

Wie groß müsste der Mittelpunktswinkel für Wasserkraft sein?
Wahlaufgaben
Aufgabe W1a:
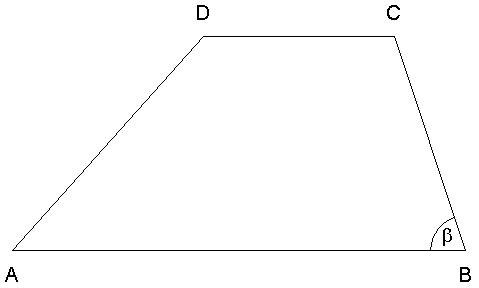
Vom Trapez ABCD sind bekannt:
Ein Punkt P liegt auf .

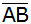Die Strecke 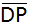halbiert die Trapezfläche.

 

Berechnen Sie die Länge .
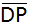5,5 P
Aufgabe W1b:
Die Dreiecke ABC und ABD haben die Seite gemeinsam.

Zeigen Sie ohne Verwendung gerundeter Werte, dass gilt:
4,5 P
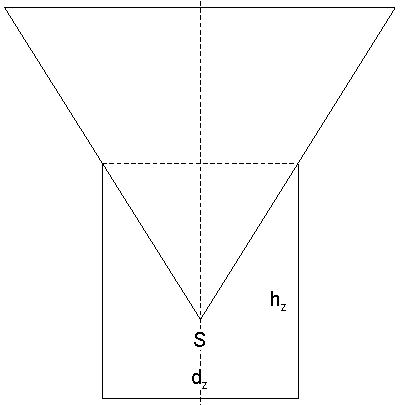
Aufgabe W2a:
Ein oben offener Zylinder ist bis zum Rand mit Wasser gefüllt.

Ein Kegel wird in das Wasser getaucht.
Er steckt dann bis zu seiner halben Höhe im Zylinder (siehe Achsenschnitt).

Bei diesem Vorgang laufen 210 cm3 Wasser aus.

Es gilt:
Berechnen Sie den Abstand der Kegelspitze S zur Grundfläche des Zylinders.

Wie viel Prozent des Kegelmantels stehen im Wasser?
5 P
 
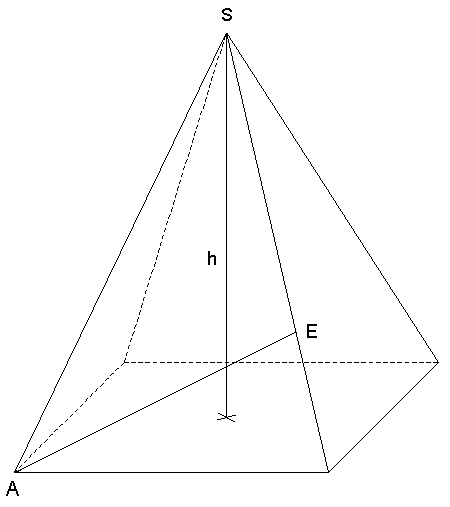
Aufgabe W2b:
Gegeben ist eine quadratische Pyramide.

Es gilt:

 
Berechnen Sie den Abstand des Punktes E von der Grundfläche.
5 P
Aufgabe W3a:
Die Parabel 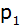mit dem Scheitel 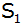hat die Gleichung .
Die Gerade hat die Gleichung .
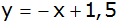Durch die beiden Schnittpunkte P und Q von 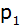und verläuft die verschobene und nach oben geöffnete Normalparabel .
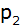Berechnen Sie die Koordinaten des Scheitelpunktes 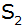von .
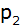Zeigen Sie rechnerisch, dass das Viereck ein Parallelogramm ist.
5,5 P
Aufgabe W3b:
Der Punkt 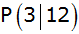liegt auf einer nach oben geöffneten Normalparabel p.
Die Parabel p hat als Symmetrieachse die Parallele zur y-Achse durch den Punkt .
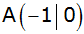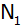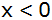Sie schneidet die x-Achse in den Punkten (mit ) und .
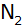Der Parabelpunkt 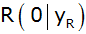sowie die Punkte P und 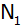bilden das Dreieck .
Berechnen Sie den Flächeninhalt des Dreiecks .
4,5 P
Aufgabe W4a:
Bei einer Wohltätigkeitsveranstaltung führt die Klasse 10a der Neckar-Realschule ein Glücksspiel durch.
Die Sektoren des dafür verwendeten Glücksrads sind rot, gelb und blau gefärbt.

Die Wahrscheinlichkeit für Rot beträgt 25%, für Gelb .
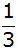Das Glücksrad wird einmal gedreht.
Folgender Gewinnplan ist vorgesehen:
Farbe Gewinn
Rot 4,00 €
Gelb 1,50 €
Blau 0,60 €
Pro Spiel werden 2,00 € Einsatz verlangt.
Berechnen Sie den Erwartungswert.
Die Klasse möchte ihren zu erwartenden Gewinn pro Spiel verdoppeln. Dabei sollen das Glücksrad und der Einsatz pro Spiel nicht verändert werden.
Stellen sie einen möglichen Gewinnplan auf.
5 P
Aufgabe W4b:
Ein Brückenbogen überspannt eine Fahrbahn und hat die Form einer nach unten geöffneten Parabel mit der Gleichung .
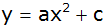Die Höhe des Bogens beträgt 5,80 m. Auf Fahrbahnhöhe ist der Brückenbogen 8,80 m breit.
Erstellen Sie die Gleichung der zugehörigen Parabel.
Ein landwirtschaftliches Fahrzeug ist 3,20 m breit und 4,60 m hoch. Kann das Fahrzeug durchfahren?
Begründen Sie Ihre Antwort.
5 P