|
Pflichtaufgaben |
|
Aufgabe P1: |
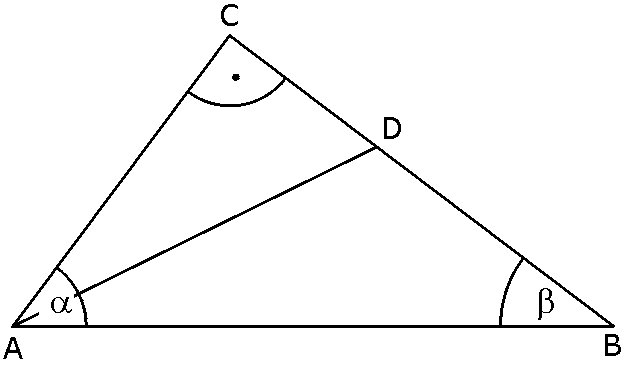
| Im
rechtwinkligen Dreieck ABC sind gegeben: |
|
|
Berechnen Sie
die Länge 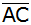 und den Abstand des Punktes D von
und den Abstand des Punktes D von
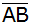 . . |
|
|
 |
4 P |
|
|
Aufgabe P2: |
| Für das
Rechteck ABCD gilt: |
|
|
Berechnen Sie
die Länge
 . . |
|
|
 |
4,5 P |
|
|
Aufgabe P3: |
| Tina
vergleicht einen Kegel und eine quadratische
Pyramide. |
| Der
Durchmesser d der Kegelgrundfläche und die
Grundkante a der quadratischen Pyramide sind
gleich lang. |
| Es
gilt: |
|
|
| Tina
meint: "Die Oberfläche der beiden Körper
sind gleich groß." |
|
Überprüfen Sie diese Aussage. |
|
|
4,5 P |
|
|
|
|
|
Aufgabe P4: |
| Bestimmen Sie
die Definitions- und die Lösungsmenge der Gleichung: |
| |
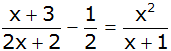 |
|
|
3 P |
|
|
Aufgabe P5: |
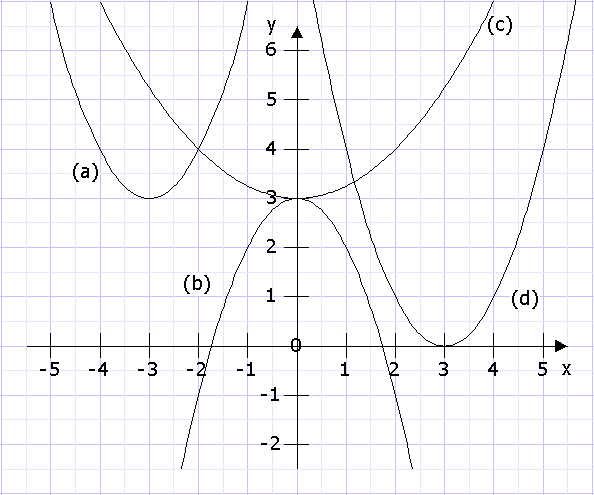
| Drei
Gleichungen - vier Graphen |
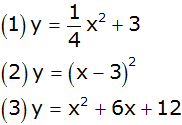 |
| Welche
Funktionsgleichung gehört zu welchem Graph? |
| Begründen Sie
Ihre Entscheidungen. |
| Wie heißt die
Funktionsgleichung des vierten Graphen? |
|
|
 |
4 P |
|
|
Aufgabe P6: |
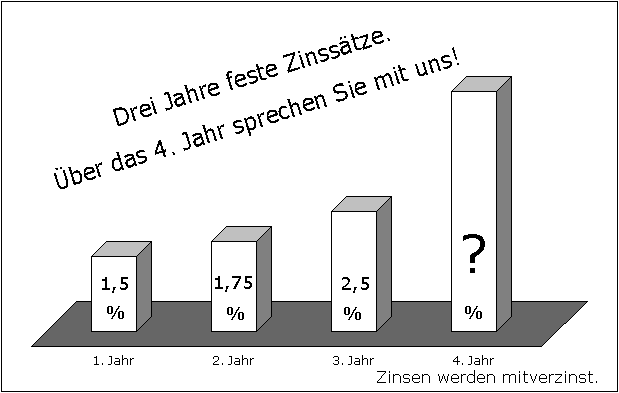
| Eine Bank
wirbt mit nebenstehender Grafik.
Herr Lenz möchte einen Betrag von 5 000,00 €
anlegen. Nach Ablauf von 4 Jahren soll sich der
Betrag auf 5 500,00 € erhöhen.
Welchen Zinssatz müsste die
Bank für das vierte Jahr anbieten?
Bei welchem jährlich
gleichbleibenden Zinssatz würde er nach vier Jahren
das gleiche Endkapital erzielen?
|
|
|
 |
3,5 P |
|
|
|
Eine Maschine füllt 1 kg-Mehltüten ab.
Bei einer Qualitätskontrolle werden die tatsächlichen Gewichte
ermittelt.
Der Boxplot zeigt das Ergebnis der erfassten Stichprobe auf Gramm
(g) gerundet. |
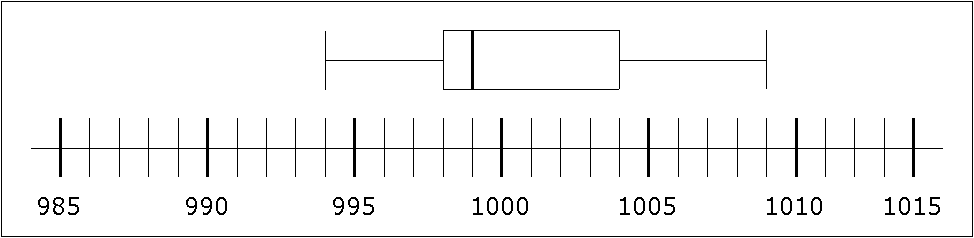 |
| Geben Sie das untere und das obere Quartil
sowie den Zentralwert an.
Nehmen Sie zu folgender Aussage
Stellung:
"Das arithmetische Mittel der Stichprobe beträgt 999 g."
|
|
|
Aufgabe P8: |
| Für eine
Geburtstagsparty werden 20 Glückskekse gebacken,
unterschiedlich gefüllt und in einen Korb gelegt. |
|
|
12 Kekse
enthalten jeweils ein Sprichwort |
|
|
6 Kekse
enthalten jeweils einen Witz |
|

|
die
restlichen werden mit jeweils einem
Kinogutschein gefüllt |
|
| Welche
Wahrscheinlichkeit hat das Ereignis "mit einem Zug
ein Sprichwort ziehen"?
Wie groß ist die
Wahrscheinlichkeit für das Ereignis "beim
gleichzeitigen Ziehen von zwei Glückskeksen
unterschiedliche Füllungen erhalten"?
|
|
|
3,5 P |
|
|
Wahlaufgaben |
|
Aufgabe W1a: |
| Im Dreieck ABC
gilt: |
|
|
| Berechnen Sie
den Flächeninhalt des Dreiecks BCD. |
|
|
 |
5,5 P |
|
|
Aufgabe W1b: |
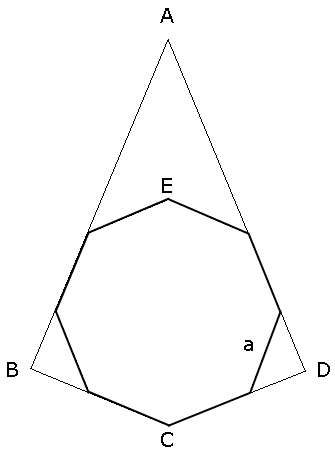
Die Figur
besteht aus einem Viereck ABCD und einem
regelmäßigen Achteck.
Außer dem Punkt E liegen
alle Eckpunkte des regelmäßigen Achtecks auf den
Seiten des Vierecks ABCD.
Weisen Sie nach, dass der
Winkel ADC ein rechter Winkel ist.
Es gilt:
|
|
|
| Berechnen Sie
den Umfang des Vierecks ABCD. |
|
|
 |
4,5 P |
|
|
Aufgabe W2a: |
| Von einer
massiven regelmäßigen fünfseitigen Pyramide sind
bekannt: |
|
|
| Ein Teil der
Pyramide wird ausgeschnitten (siehe Skizze).
Berechnen Sie die Oberfläche
des neu entstandenen Körpers.
|
|
|
 |
6 P |
|
|
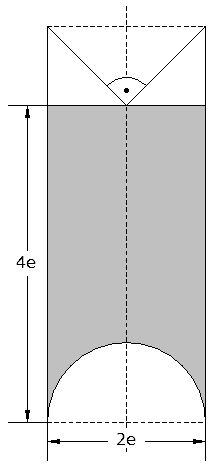
Aufgabe W2b: |
Ein
zylinderförmiges Gefäß hat eine kegelförmige und
eine halbkugelförmige Vertiefung.
Das Wasser
reicht genau bis zur Spitze der kegelförmigen
Vertiefung (siehe Achsenschnitt).
Das Gefäß wird gedreht und
auf die kegelförmige Vertiefung gestellt.
|
| |
| Zeigen Sie ohne
Verwendung gerundeter Werte, dass die Höhe des
Wasserstands dadurch |
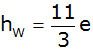 beträgt.
beträgt. |
|
|
 |
4 P |
|
|
|
|
|
|
|
Die Abschlussklassen der Linden-Realschule
organisieren zugunsten eines sozialen Projekts eine Tombola.
Die
Tabelle zeigt die Losverteilung und die damit jeweils verbundenen
Gewinne. |
 |
| Ein Los kostet 2,00 €.
Berechnen Sie den Erwartungswert.
Um den Gewinn für das soziale Projekt zu erhöhen, geben die
Klassen 50 weitere Nieten in die Lostrommel.
Welchen Betrag können die Abschlussklassen
spenden, wenn alle Lose verkauft werden?
|
|
|
|