Die
Parabel
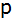 mit der Gleichung
mit der Gleichung
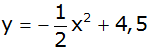 schneidet die x-Achse in den Punkten
schneidet die x-Achse in den Punkten
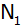 und
und
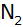 .
Die Gerade .
Die Gerade
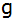 verläuft durch den rechten Schnittpunkt der
Parabel mit der x-Achse und hat die Steigung
verläuft durch den rechten Schnittpunkt der
Parabel mit der x-Achse und hat die Steigung
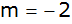 . .
Berechnen Sie den zweiten Schnittpunkt
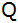 der Geraden
der Geraden
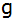 mit der Parabel
mit der Parabel
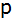 . .
Die Punkte
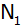 und
und
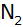 sowie der Punkt
sowie der Punkt
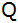 bilden ein Dreieck.
bilden ein Dreieck.
Berechnen Sie den Flächeninhalt des
Dreiecks.
Der Punkt
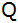 bewegt sich jetzt oberhalb der x-Achse auf
der Parabel
bewegt sich jetzt oberhalb der x-Achse auf
der Parabel
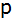 . .
Für welche Lage von
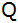 wird der Flächeninhalt des Dreiecks am
größten?
wird der Flächeninhalt des Dreiecks am
größten?
|