|
Aufgabe 1a: |
| In einer
arithmetischen Reihe beträgt die Summe aus dem
zweiten und fünften Glied 112 und die Summe aus dem
dritten und achten Glied 144. |
|
Berechne das Anfangsglied, die Differenz und die
Summe der ersten zehn Glieder dieser Reihe. |
|
|
4 P |
|
|
Aufgabe 1b: |
In einer
arithmetischen Reihe mit
 und
und
 ist die Summe der ersten n Glieder fünfmal so groß
ist die Summe der ersten n Glieder fünfmal so groß
wie das Glied
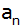 . . |
Bestimme n,
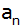 und
und
 dieser Reihe.
dieser Reihe. |
|
|
4 P |
|
|
Aufgabe 1c: |
Addiert man zu
jedem Glied einer arithmetischen Reihe, in der
 und
und
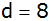 ist, eine Zahl c, so entsteht
ist, eine Zahl c, so entsteht
eine neue
arithmetische Reihe mit
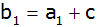 , ,
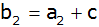 , ,
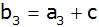 usw.
usw. |
Ermittle, für welches c die Beziehung
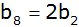 gilt.
gilt. |
|
|
3 P |
|
|
Aufgabe 2a: |
| Entscheide, ob
es sich bei diesen Zahlenfolgen um arithmetische
Folgen oder geometrische Folgen handelt: |
|
|
|
Bestimme jeweils d bzw. q und ergänze jede
Zahlenfolge um die folgenden zwei Glieder. |
|
|
4 P |
|
|
Aufgabe 2b: |
Eine
arithmetische Reihe mit der Differenz d = 5 und eine
geometrische Reihe haben beide das Anfangs-
glied 2,
gleich viele Glieder und dasselbe Endglied 52. |
|
Berechne sowohl den Quotienten als auch die Summe
der geometrischen Reihe. |
|
|
4 P |
|
|
Aufgabe 2c: |
Die Differenz des dritten und ersten Gliedes einer
geometrischen Reihe beträgt 40v, die Summe des
zweiten und ersten Gliedes ist 20v. |
| 1. |
Berechne
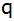 ,
wenn ,
wenn
 gilt.
gilt. |
| 2. |
Für welche Zahl v wird die Summe der
ersten 5 Glieder dieser Reihe 4235? |
|
|
|
3 P |
|
|
Aufgabe 3a: |
In einem rechtwinkligen Koordinatensystem
(Längeneinheit = 1cm) ist ein Dreieck durch die
Eckpunkte
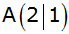 , ,
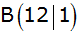 und
und
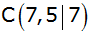 gegeben.
gegeben. |
|
Zeichne das Dreieck. |
|
|
1 P |
|
|
Aufgabe 3b: |
In einem rechtwinkligen Koordinatensystem
(Längeneinheit = 1cm) ist ein Dreieck durch die
Eckpunkte
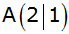 , ,
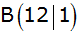 und
und
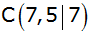 gegeben.
gegeben. |
Berechne die Seiten a, b, c und die Winkel
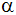 , ,
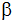 , ,
 dieses Dreiecks.
dieses Dreiecks. |
|
|
3 P |
|
|
Aufgabe 3c: |
In einem rechtwinkligen Koordinatensystem
(Längeneinheit = 1cm) ist ein Dreieck durch die
Eckpunkte
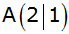 , ,
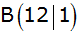 und
und
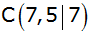 gegeben.
gegeben. |
Das Dreieck rotiert um die Achse
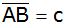 ,
bestimme das Volumen des Drehkörpers. ,
bestimme das Volumen des Drehkörpers. |
|
|
3 P |
|
|
Aufgabe 3d: |
In einem rechtwinkligen Koordinatensystem
(Längeneinheit = 1cm) ist ein Dreieck durch die
Eckpunkte
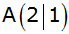 , ,
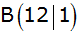 und
und
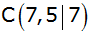 gegeben.
gegeben. |
Um einen Punkt
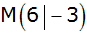 wird ein Kreis mit r = 5cm beschrieben.
wird ein Kreis mit r = 5cm beschrieben. |
|
Dieser Kreis schneidet aus dem Dreieck eine
Kreisabschnittsfläche heraus. |
|
Berechne die Restfläche des Dreiecks ABC. |
|
|
3 P |
|
|
Aufgabe 3e: |
Ein Dreieck ABC' ist durch die Eckpunkte
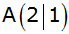 , ,
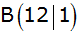 und
und
 gegeben,
gegeben,
wobei
 gilt.
gilt. |
|
Das Dreieck rotiert um eine Achse, die parallel zur
x-Achse durch den Punkt C' verläuft. |
| 1. |
Berechne das Volumen
 des Drehkörpers.
des Drehkörpers. |
| 2. |
Für welchen Wert a beträgt das Volumen
des Drehkörpers
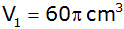 ?
? |
|
|
|
3 P |
|
|
Aufgabe 4a: |
Von einem Trapez sind die Längen der Strecken
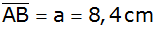 , ,
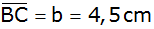 und
und
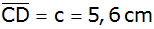 ,
sowie die Höhe ,
sowie die Höhe
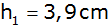 bekannt.
bekannt. |
|
Zeichne das Trapez. |
|
|
1 P |
|
|
Aufgabe 4b: |
Von einem Trapez sind die Längen der Strecken
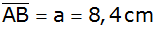 , ,
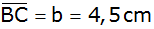 und
und
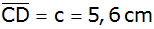 ,
sowie die Höhe ,
sowie die Höhe
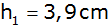 bekannt.
bekannt. |
Berechne die Länge der Diagonalen
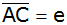 . . |
|
|
2 P |
|
|
Aufgabe 4c: |
Von einem Trapez sind die Längen der Strecken
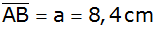 , ,
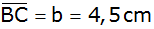 und
und
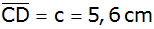 ,
sowie die Höhe ,
sowie die Höhe
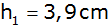 bekannt.
bekannt. |
|
Wie groß ist der Flächeninhalt des Trapezes? |
|
|
1 P |
|
|
Aufgabe 4d: |
Von einem Trapez sind die Längen der Strecken
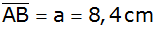 , ,
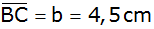 und
und
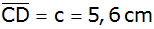 ,
sowie die Höhe ,
sowie die Höhe
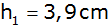 bekannt.
bekannt. |
Verlängert man
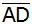 über D hinaus und
über D hinaus und
 über C hinaus, so schneiden sich die Verlängerungen
in F.
über C hinaus, so schneiden sich die Verlängerungen
in F. |
Berechne sowohl die Höhe
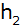 des Dreiecks ABF als auch die Größe des Winkels
des Dreiecks ABF als auch die Größe des Winkels
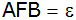 . . |
|
|
2 P |
|
|
Aufgabe 4e: |
Von einem Trapez sind die Längen der Strecken
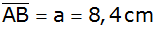 , ,
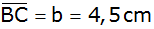 und
und
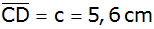 ,
sowie die Höhe ,
sowie die Höhe
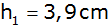 bekannt.
bekannt. |
Eine Parallele zu
 durch D schneidet
durch D schneidet
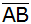 in G und
in G und
 in H.
in H. |
| 1. |
Wie lang ist die Strecke
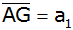 ,
und in welchem Verhältnis steht sie zur
Strecke ,
und in welchem Verhältnis steht sie zur
Strecke
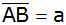 ? ? |
| 2. |
Wie groß ist die Höhe
 des Dreiecks AGH, und in welchem Verhältnis
steht sie zur Höhe
des Dreiecks AGH, und in welchem Verhältnis
steht sie zur Höhe
 des Dreiecks ABC?
des Dreiecks ABC? |
| 3. |
Welchen Inhalt haben die Flächen
 und
und
 der Dreiecke ABC und AGH, und in welchem
Verhältnis stehen sie zueinander?
der Dreiecke ABC und AGH, und in welchem
Verhältnis stehen sie zueinander? |
|
|
|
3 P |
|
|
Aufgabe 5a: |
Von einem
Dreieck sind die Winkel
 und
und
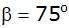 ,
sowie die Seite ,
sowie die Seite
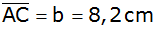 gegeben.
gegeben. |
| Konstruiere das
Dreieck ABC und den Umkreismittelpunkt M. |
Berechne die
Seiten
 und
und
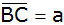 ,
sowie die Länge des Umkreisradius r. ,
sowie die Länge des Umkreisradius r. |
|
|
4 P |
|
|
Aufgabe 5b: |
Von einem
Dreieck sind die Winkel
 und
und
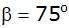 ,
sowie die Seite ,
sowie die Seite
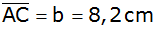 gegeben.
gegeben. |
Außerhalb des
Dreiecks ABC liegt ein Punkt D mit
 . . |
Berechne die
Strecke
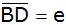 . . |
|
|
4 P |
|
|
Aufgabe 5c: |
Von einem
Dreieck sind die Winkel
 und
und
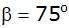 ,
sowie die Seite ,
sowie die Seite
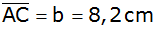 gegeben.
gegeben. |
Außerhalb des
Dreiecks ABC liegt ein Punkt D mit
 . . |
Die Gerade
 schneidet
schneidet
 in E.
in E. |
Begründe,
weshalb D und M auf der Mittelsenkrechten von
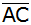 liegen, und berechne sowohl den Umfang als
liegen, und berechne sowohl den Umfang als
auch
den Inhalt des Dreiecks ADE. |
|
|
3 P |
|
|
Aufgabe 6a: |
| Ein
quaderförmiges Gefäß mit quadratischer Grundfläche
faßt genau 1 Liter. |
Berechne die
Höhe h des Gefäßes, wenn die Grundkante
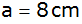 mißt.
mißt. |
|
|
1 P |
|
|
Aufgabe 6b: |
| Ein
quaderförmiges Gefäß mit quadratischer Grundfläche
faßt genau 1 Liter. |
| Das Gefäß ist
ganz mit Wasser gefüllt. |
Wieviel Prozent
der Wassermenge verdrängt eine voll eingetauchte
Kugel
 ,
wenn diese möglichst ,
wenn diese möglichst
groß sein soll? |
|
|
2 P |
|
|
Aufgabe 6c: |
| Ein
quaderförmiges Gefäß mit quadratischer Grundfläche
faßt genau 1 Liter. |
| Das Gefäß ist
halb mit Wasser gefüllt. |
Um wieviel
Zentimeter steigt der Wasserspiegel, wenn eine Kugel
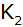 mit dem Radius
mit dem Radius
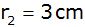 voll
voll
eingetaucht wird? |
|
|
3 P |
|
|
Aufgabe 6d: |
Welches
Raumverhältnis besteht zwischen einem Würfel mit der
Kantenlänge
 und einer Kugel
und einer Kugel
mit dem Radius
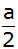 ? ? |
|
|
2 P |
|
|
Aufgabe 7a: |
Ein
rechtwinkliges Dreieck besitzt die Katheten
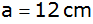 und
und
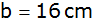 . . |
Bei der
Rotation um Kathete
 erzeugt es einen Drehkörper mit dem Volumen
erzeugt es einen Drehkörper mit dem Volumen
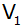 und der Mantelfläche
und der Mantelfläche
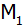 , , |
bei der
Rotation um Kathete
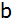 erzeugt es einen Drehkörper mit dem Volumen
erzeugt es einen Drehkörper mit dem Volumen
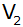 und der Mantelfläche
und der Mantelfläche
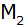 . . |
| In welchem
Verhältnis stehen die beiden Rauminhalte, und wie
groß sind die beiden Mantelflächen? |
|
|
4 P |
|
|
Aufgabe 7b: |
Ein
rechtwinkliges Dreieck mit der Hypotenuse
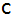 und der Höhe
und der Höhe
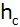 rotiert um die Hypotenuse.
rotiert um die Hypotenuse. |
|
1. |
Wie groß ist das Volumen
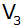 des Rotationskörpers, wenn
des Rotationskörpers, wenn
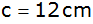 und
und
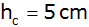 sind?
sind? |
|
2. |
Wenn
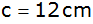 ist, wie groß muss dann
ist, wie groß muss dann
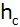 sein, damit das Volumen
sein, damit das Volumen
 genau
genau
 wird?
wird? |
|
|
|
4 P |
|
|
Aufgabe 7c: |
In einem
spitzwinkligen Dreieck ABC sind die Winkel
 und
und
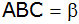 ,
sowie die Höhe ,
sowie die Höhe
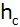
gegeben. |
Wie groß ist
das Volumen
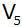 des Rotationskörpers, das bei Drehung um
des Rotationskörpers, das bei Drehung um
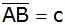 entsteht?
entsteht? |
|
|
3 P |
|
|
Aufgabe 8a: |
Von einem quadratischen Pyramidenstumpf sind die Länge der
Grundseite
 , die
Länge der , die
Länge der
Deckkante
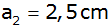 und die
Länge der Seitenkante und die
Länge der Seitenkante
 bekannt.
bekannt. |
|
Wie groß ist das Volumen dieses Pyramidenstumpfes? |
|
4 P |
|
|
Aufgabe 8b: |
Ein quadratischer Pyramidenstumpf mit den Maßen
 , ,
 und und
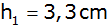 wird
zur Pyramide ergänzt. wird
zur Pyramide ergänzt. |
| 1. |
Berechne das Volumen des Pyramidenstumpfes. |
| 2. |
Berechne sowohl die Höhe als auch das Volumen
der Ergänzungspyramide. |
| 3. |
In welchem Verhältnis stehen Körperhöhen und
Rauminhalte beider Körper? |
|
|
4 P |
|
|
Aufgabe 8c: |
Einem quadratischen Pyramidenstumpf mit den Maßen
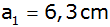 , ,
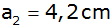 und und
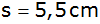
wird
eine Kugel umbeschrieben. |
|
Wie groß sind der Radius und das Volumen dieser Umkugel? |
|
3 P |
|