| 1. Berechnung der
Wahrscheinlichkeit für zwei gleichfarbige Kugeln: |
| Für unsere
Aufgabe gibt es 8 mögliche Ereignisse. |
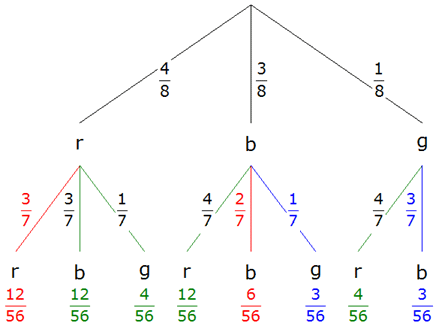
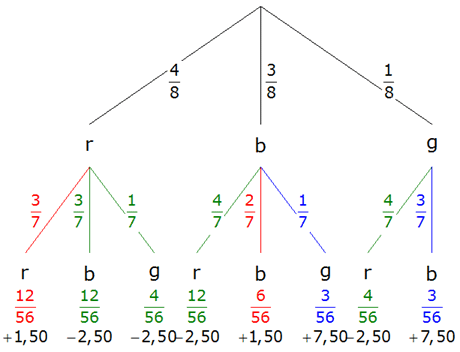
| Das
Experiment wird durch einen
Ereignisbaum
dargestellt. |
| Für die erste
Kugel ergeben sich folgende Wahrscheinlichkeiten: |
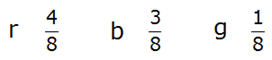 |
| Ist die erste
Kugel rot, so ergeben sich für die zweite Kugel folgende Wahrscheinlichkeiten: |
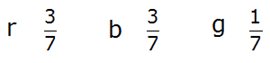 |
|
Ist die erste Kugel blau, so ergeben sich für die
zweite Kugel folgende Wahrscheinlichkeiten: |
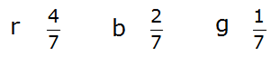 |
|
Ist die erste Kugel gelb, so ergeben sich
für die zweite Kugel folgende Wahrscheinlichkeiten: |
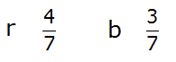 |
|
|
 |
| Für das Ereignis zwei
gleichfarbige Kugeln zu ziehen, ergeben sich folgende
Wahrscheinlichkeiten: |
|
r r |
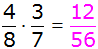 |
|
b b |
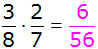 |
|
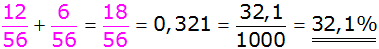 |
| Antwort: Die
Wahrscheinlichkeit zwei gleichfarbige Kugeln zu ziehen,
beträgt 32,1%. |
|
 |
| 2. Berechnung des
Erwartungswertes: |
|
Der Erwartungswert E berechnet sich nach folgender
Formel: |
|
 |
|
wobei |
|
 |
|
Für dieses Glücksspiel gibt es n = 3 mögliche
Ereignisse |
|
1.
zwei gleichfarbige
Kugeln:
r r oder
b b |
|
2.
Eine gelbe und
eine blaue Kugel:
b g
oder
g b |
|
3. restliche Möglichkeiten:
alle anderen |
|
|
 |
|
|
|
|
Es ergeben sich folgende Gewinnwerte: |
|
r
r
b b
|
Gleichfarbige
Kugeln: man hat einen Gewinn von 4 €, muss
aber den Kaufpreis von 2,50 € abziehen |
+ 1,50 |
|
b g
g
b
|
Gelbe und
blaue Kugel: man hat einen Gewinn von 10 €, muss aber den Kaufpreis
von 2,50 € abziehen |
+ 7,50 |
| alle
anderen |
man verliert
den Einsatz von 2,50 € |
- 2,50 |
|
 |
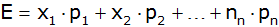 |
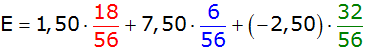 |
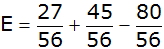 |
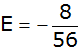 |
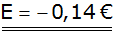 |
|
Antwort: Der Erwartungswert beträgt - 0,14 €. |
|
|
| 3. Abänderung des
Gewinnplans für Verdopplung des Gewinns für den Veranstalter: |
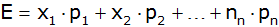 |
|
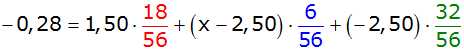 |
|
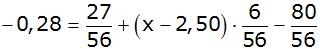 |
|
 |
Seiten tauschen |
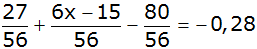 |
 |
 |
 |
 |
|
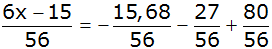 |
|
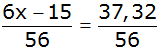 |
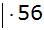 |
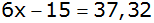 |
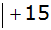 |
 |
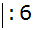 |
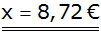 |
|
|
Antwort: Für die
Verdopplung des Gewinns für den Veranstalter müsste
der Gewinn für eine gelbe und eine blaue Kugel 8,72 € betragen. |
|
|
|



