1. Berechnung der
Koordinaten der Schnittpunkte
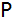 und
und
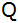 : : |
 |
Gleichsetzungsverfahren |
 |
 |
 |
Zusammenfassen |
 |
Normalform einer
quadratischen Gleichung |
 |
|
 |
|
 |
p und q bestimmen |
 |
Lösungsformel |
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
 |
 |
 |
|
|
|
 |
2. Berechnung der Koordinaten
des Scheitelpunktes
 von von
 : : |
 |
Allgemeine Parabelgleichung |
|
|
 |
|
|
Punktkoordinaten einsetzen |
 |
|
 |
Seiten tauschen |
 |
 |
 |
Gleichsetzverfahren |
 |
 |
 |
 |
 |
 |
 |
|
 |
p = 2 in II' einsetzen |
 |
|
 |
|
 |
Quadratische Ergänzung |
 |
|
 |
|
 |
|
 |
Scheitelgleichung |
 |
|
 |
|
 |
|
 |
|
|
|
 |
| 3. Überprüfung von Robins
Behauptung: |
 |
|
 |
|
 |
 |
 |
|
 |
|
 |
|
 |
 |
 |
|
 |
|
 |
|
 |
 |
 |
|
 |
Wenn der Satz des Pythagoras erfüllt wird, ist das
Dreieck rechtwinklig |
 |
|
 |
|
 |
|
|
Antwort: |
Robin hat nicht
recht. Da der Satz von Pythagoras von dem
Dreieck PQS2 nicht erfüllt wird,
ist das Dreieck nicht rechtwinklig. |
|
|
|
 |


