1. Berechnung des
Erwartungswertes
 : |
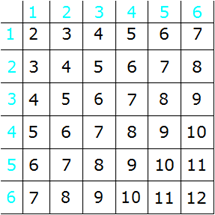
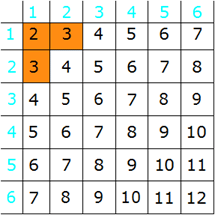
| Für das Werfen
zweier Würfel gibt es insgesamt 36 mögliche Ereignisse. |
|
|
 |
|
|
 |
|
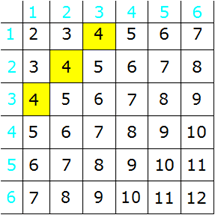
Für das Ereignis "Augensumme
kleiner 4" gibt es drei Möglichkeiten: |
| |
|
| |
 |
| |
|
 |
|
 |
|
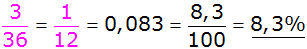Es ergeben sich folgende Wahrscheinlichkeiten: |
|
gleich 4 |
 |
|
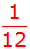kleiner 4 |
 |
|
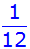alle anderen |
 |
|
|
|
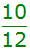Es ergeben sich folgende Gewinnwerte: |
|
gleich 4
|
man
hat einen Gewinn von 4 €, muß aber den Kaufpreis von 1 €
abziehen |
+ 3 |
|
kleiner 4
|
man
hat man einen Gewinn von 2 €, muß aber den Kaufpreis von
1 € abziehen |
+ 1 |
|
alle anderen |
man
verliert den Einsatz von 1 € |
- 1 |
|
|
 |
 |
 |
 |
 |
|
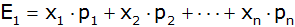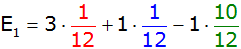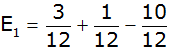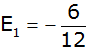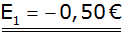Antwort: Der Erwartungswert beträgt
- 0,50 € |
|
|
2. Berechnung des
Erwartungswertes
mit drei weiteren Einsen: |
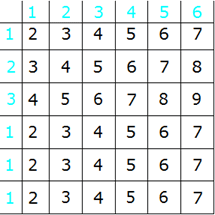
| Für das Werfen der zwei Würfel gibt
es wieder insgesamt 36 mögliche Ereignisse. |
|
 |
|
Für das Ereignis "Augensumme
gleich 4" gibt es sechs Möglichkeiten: |
| |
 |
| |
|
| |
|
|
|
| |
|
| |
|
 |
|
 |
|
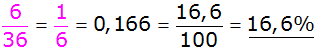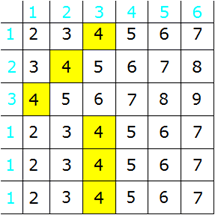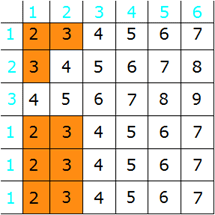
Für das Ereignis "Augensumme
kleiner 4" gibt es neun Möglichkeiten: |
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
 |
|
 |
|
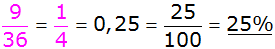Es ergeben sich folgende Wahrscheinlichkeiten: |
|
gleich 4 |
 |
|
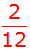kleiner 4 |
 |
|
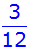alle anderen |
 |
|
|
|
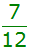Es ergeben sich folgende Gewinnwerte: |
|
gleich 4
|
man
hat einen Gewinn von 4 €, muß aber den Kaufpreis von 1 €
abziehen |
+ 3 |
|
kleiner 4
|
man
hat man einen Gewinn von 2 €, muß aber den Kaufpreis von
1 € abziehen |
+ 1 |
|
alle anderen |
man
verliert den Einsatz von 1 € |
- 1 |
|
|
|
|
|
3. Berechnung des
Erwartungswertes
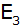mit drei weiteren Dreien: |
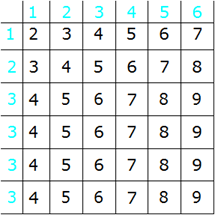
| Für das Werfen der zwei Würfel gibt
es wieder insgesamt 36 mögliche Ereignisse. |
|
 |
|
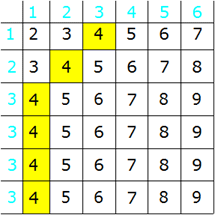
Für das Ereignis "Augensumme
gleich 4" gibt es sechs Möglichkeiten: |
| |
|
| |
|
| |
|
|
|
| |
|
| |
|
|
|
|
 |
|
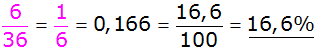Für das Ereignis "Augensumme
kleiner 4" gibt es drei Möglichkeiten: |
| |
|
| |
|
| |
|
| |
|
|
|
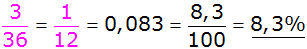Es ergeben sich folgende Wahrscheinlichkeiten: |
|
gleich 4 |
 |
|
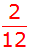kleiner 4 |
|
|
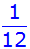alle anderen |
 |
|
|
|
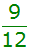Es ergeben sich folgende Gewinnwerte: |
|
gleich 4
|
man
hat einen Gewinn von 4 €, muß aber den Kaufpreis von 1 €
abziehen |
+ 3 |
|
kleiner 4
|
man
hat man einen Gewinn von 2 €, muß aber den Kaufpreis von
1 € abziehen |
+ 1 |
|
alle anderen |
man
verliert den Einsatz von 1 € |
- 1 |
|
|
|
|
|
|
Antwort: Der Betreiber sollte sich
für die Ergänzung mit drei Dreien entscheiden, da der Erwartungswert
negativ ist. |
|
Argumentative Begründung:
Ersetzt der Betreiber auf einem der beiden Würfel die Vier, die Fünf
und die Sechs durch drei Einsen, dann gibt es insgesamt 9 mögliche
Ereignisse "Augensumme kleiner 4". Werden drei Dreien hinzugefügt,
ergeben sich insgesamt nur 3 mögliche Ereignisse "Augensumme kleiner
4". Die Anzahl der möglichen Ereignisse "Augensumme gleich 4" ist in
beiden Fällen gleich.
Deshalb
sollte sich der Betreiber für die drei Dreien entscheiden. |
|
