1. Berechnung der
Wahrscheinlichkeit höchstens einmal das Symbol
zu erhalten: |
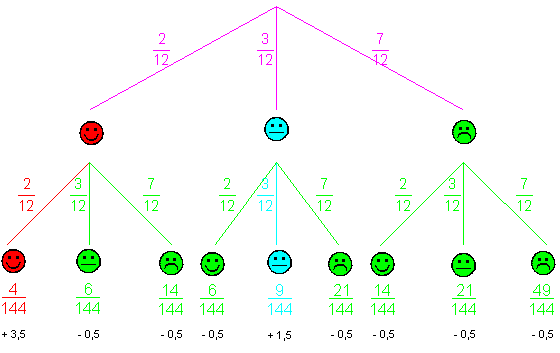
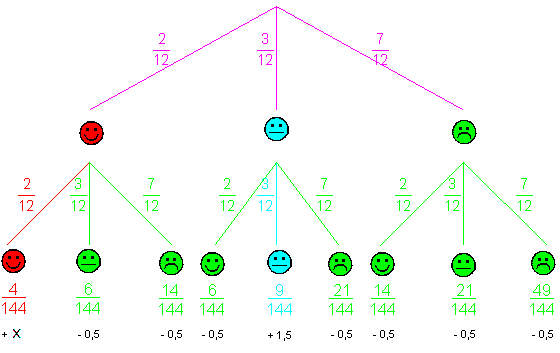
| Für unsere
Aufgabe gibt es 9 mögliche Ereignisse. |
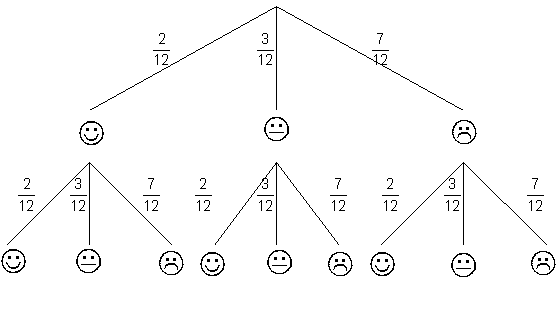
| Das
Experiment wird durch einen
Ereignisbaum
dargestellt. |
| Es ergeben sich
folgende Wahrscheinlichkeiten: |
 |
|
|
 |
|
|
 |
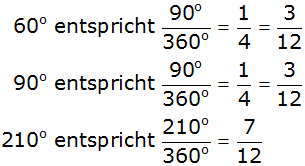| 2. Berechnung des
Erwartungswertes: |
|
Der Erwartungswert E berechnet sich nach folgender
Formel: |
|
 |
|
wobei |
|
 |
|
Für dieses Glücksspiel gibt es n = 3 mögliche
Ereignisse |
|
1.
zweimal
|
2.
zweimal:
 |
|
3. sonstige: alle
anderen |
|
|
 |
|
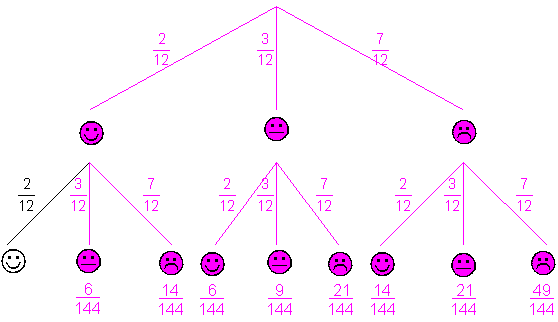
Es ergeben sich folgende Wahrscheinlichkeiten: |
|
|
 |
|
|
 |
|
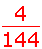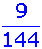alle anderen |
 |
|
|
|
|
 |
 |
 |
 |
 |
 |
|
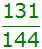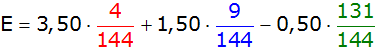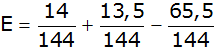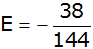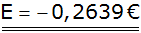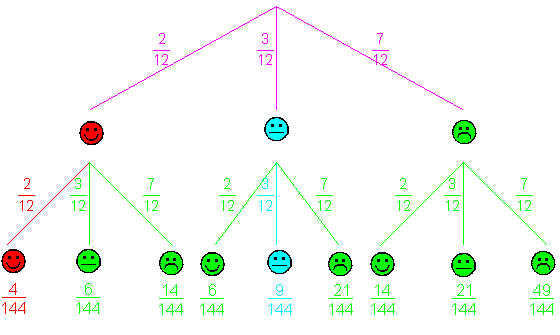
Antwort: Der Erwartungswert beträgt
- 0,26 € |
|
|
| 3. Faires
Spiel: |
|
| Der Erwartungswert E
berechnet sich nach folgender Formel: |
|
|
| wobei |
|
|
|
 |
Das Spiel ist
fair, wenn
E = 0 |
 |
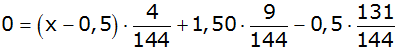Seiten
tauschen |
 |
|
 |
 |
 |
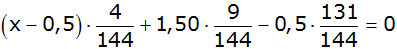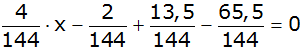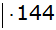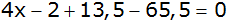Zusammenfassen |
 |
 |
 |
 |
 |
|
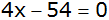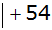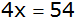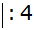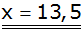Antwort: Ein
faires Spiel erhält man, wenn man für "2 mal
 "
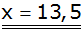einen Gewinn von 13,50 € erhält. |
|
 |
