Home Geschichte Informatik Lernmaterial Linkliste Mathematik Smartphone ARS LB
Lösung 2015 W1b
nach oben Aufgabe Strategie
Rechnerische Lösung
1. Berechnung des Umfangs :
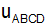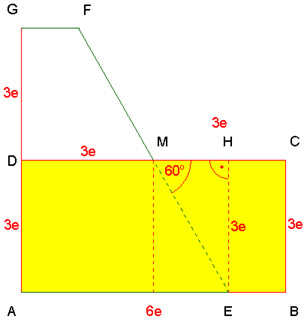
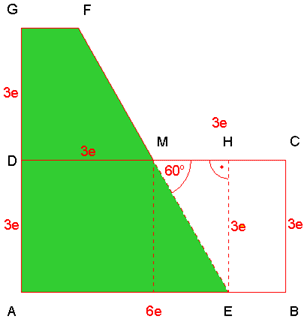
siehe gelbes Rechteck ABCD
 
 
 
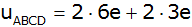2. Berechnung der Strecke :
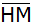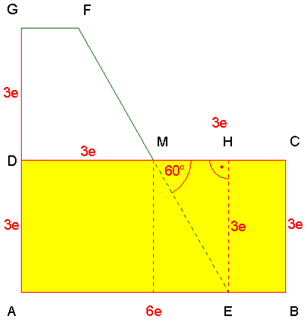
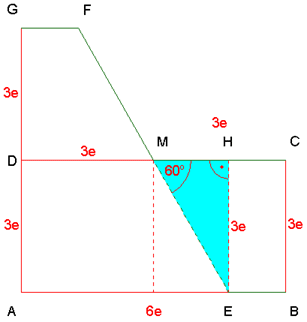
Tangensfunktion im rechtwinkligen hellblauen Teildreieck EHM
 
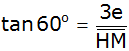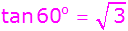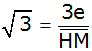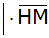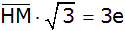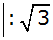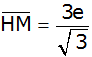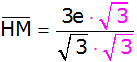Nenner rational machen
 
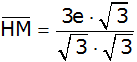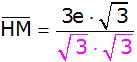Zusammenfassen
 
 
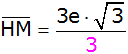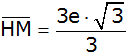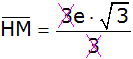Bruch kürzen
 
3. Berechnung der Strecke :
siehe goldfarbenes Trapez EBCM
 
 
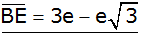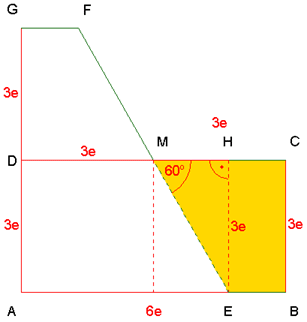4. Berechnung der Strecke :
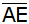siehe gelbes Rechteck ABCD
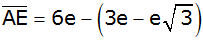Minusklammer auflösen
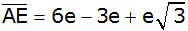Zusammenfassen
 
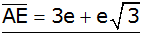5. Berechnung der Strecke :
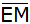Sinusfunktion im rechtwinkligen hellblauen Teildreieck EHM
   
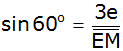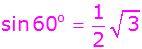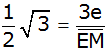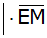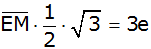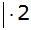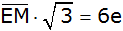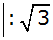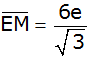  Nenner rational machen 
   
   
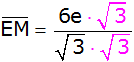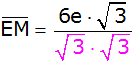  Zusammenfassen 
   
   
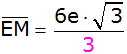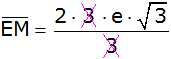  Kürzen 
   
6. Berechnung der Strecke : 
   
   
 
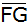7. Berechnung der Strecke : 
   
   
 
8. Berechnung des Umfangs : 
   
   
   
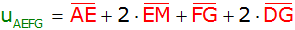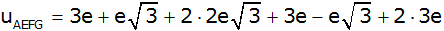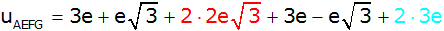  Zusammenfassen 
   
   
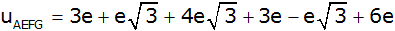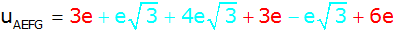  Zusammenfassen 
   
   
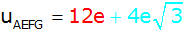  Gemeinsamen Faktor ausklammern
   
   
   
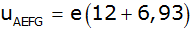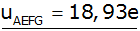9. Berechnung der Differenz : 
   
   
   
Antwort: Bea hat nicht Recht, da der Umfang des Trapezes AEFG länger ist als der Umfang des Rechtecks ABCD
 
Lösung durch Argumentation
Das Rechteck ABCD und das Trapez AEFG stimmen in den Längen 1, 2, 3 und 6 überein.
Somit müssen nur die Längen 4 + 5 und 7 + 8 verglichen werden.
Da 4 + 5 gleich lang wie 3 + 6 ist, kann man 3 + 6 mit 7 + 8 vergleichen.
Da  3 + 6 die Höhe im Trapez ist und 7 + 8 die Seite, sieht man, daß die Seite 7 + 8 länger ist als die Höhe 3 + 6.
Das bedeutet, daß der Umfang des Trapezes länger als der Umfang des Rechteckes ist.
Bea hat nicht Recht.