Lösung 2015 P4

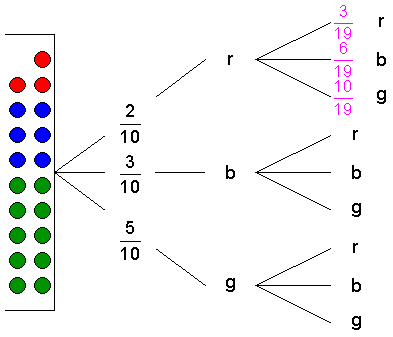
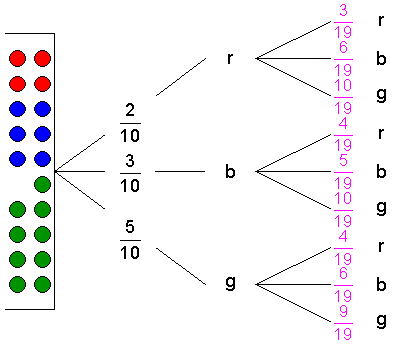
1. Vervollständigung des Baumdiagramms:

Die Wahrscheinlichkeit 20% für die roten Kugeln besagt, dass 20 pro 100 oder 2 pro 10 Kugeln rot sind. Also sind 4 von den 20 Kugeln rot.
Die Wahrscheinlichkeit

für die blauen Kugeln besagt, dass 6 von den 20 Kugeln blau sind.

Das bedeutet, dass 10 Kugeln grün sind. Die Wahrscheinlichkeit dass beim ersten Ziehen eine grüne Kugel gezogen wird beträgt also bzw. .

Wird beim ersten Ziehen eine rote Kugel ohne Zurücklegen gezogen, so befinden sich in dem Behälter 19 Kugeln. Davon sind 3 rot, 6 blau und 10 grün. Es ergeben sich folgende Wahrscheinlichkeiten:
r
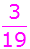b
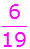g

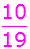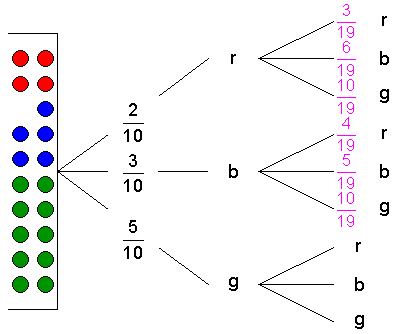
Wird beim ersten Ziehen eine blaue Kugel ohne Zurücklegen gezogen, so befinden sich in dem Behälter 19 Kugeln. Davon sind 4 rot, 5 blau und 10 grün. Es ergeben sich folgende Wahrscheinlichkeiten:
r
b
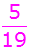g

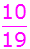Wird beim ersten Ziehen eine grüne Kugel ohne Zurücklegen gezogen, so befinden sich in dem Behälter 19 Kugeln. Davon sind 4 rot, 6 blau und 9 grün. Es ergeben sich folgende Wahrscheinlichkeiten:
r
b
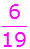g

2. Berechnung der Wahrscheinlichkeit höchstens eine grüne Kugel zu ziehen:

Es ergeben sich folgende Wahrscheinlichkeiten:

Antwort: Die Wahrscheinlichkeit, höchstens eine grüne Kugel zu ziehen, beträgt 76,3%.

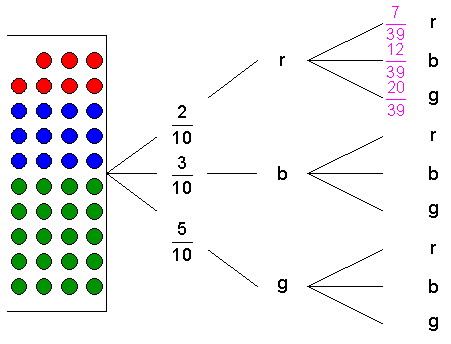
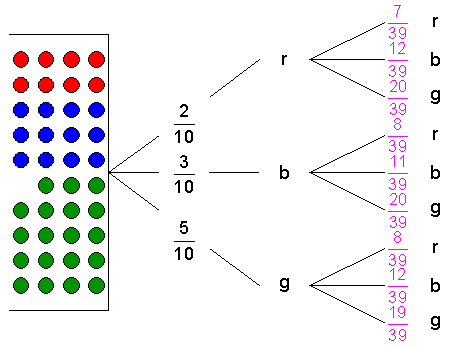
Werden die Kugeln verdoppelt, so ergeben sich für die erste Ziehung die gleichen Wahrscheinlichkeiten:
r
b
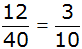g

Wird beim ersten Ziehen eine rote Kugel ohne Zurücklegen gezogen, so befinden sich in dem Behälter 39 Kugeln. Davon sind 7 rot, 12 blau und 20 grün. Es ergeben sich folgende Wahrscheinlichkeiten:
r
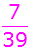b
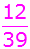g

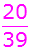Wird beim ersten Ziehen eine blaue Kugel ohne Zurücklegen gezogen, so befinden sich in dem Behälter 39 Kugeln. Davon sind 8 rot, 11 blau und 20 grün. Es ergeben sich folgende Wahrscheinlichkeiten:
r
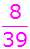b
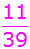g

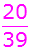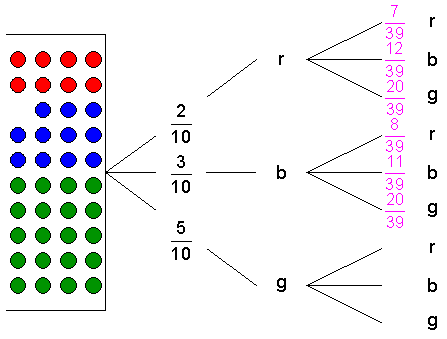Wird beim ersten Ziehen eine grüne Kugel ohne Zurücklegen gezogen, so befinden sich in dem Behälter 39 Kugeln. Davon sind 8 rot, 12 blau und 19 grün. Es ergeben sich folgende Wahrscheinlichkeiten:
r
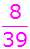b
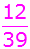g

3. Berechnung der Wahrscheinlichkeit höchstens eine grüne Kugel zu ziehen:

Es ergeben sich folgende Wahrscheinlichkeiten:

Antwort: Die Wahrscheinlichkeit, höchstens eine grüne Kugel zu ziehen, beträgt 75,6%.

Uli hat nicht Recht!!!!