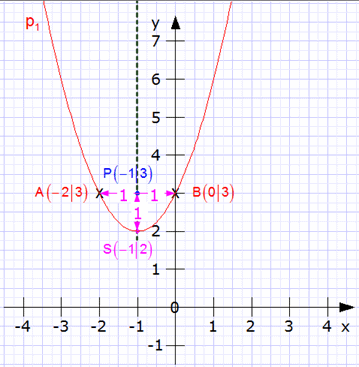
| 1. Ablesen der Koordinaten
aus dem Schaubild: |
|
|
| 2.a Bestimmung der
Parabelgleichung durch Argumentation: |
Die Symmetrieachse der Parabel
ist eine Parallele zur y-Achse. A hat zu dieser
Symmetrieachse den Abstand 1. Also hat B auch den Abstand 1
von der Symmetrieachse. Bei 1 Schritt in x-Richtung muss man
1 Schritt in y-Richtung gehen. Somit ergibt sich für den
Scheitelpunkt
 . |
 |
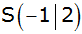Scheitelgleichung |
 |
Scheitelkoordinaten einsetzen |
 |
|
 |
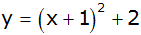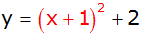1.
binomische Formel |
 |
|
 |
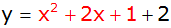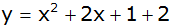Zusammenfassen |
 |
|
|
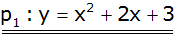| 2.b Bestimmung der
Parabelgleichung durch Berechnung: |
 |
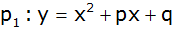Allgemeine Parabelgleichung
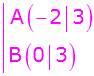
Punktkoordinaten einsetzen |
 |
|
 |
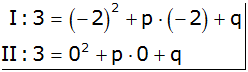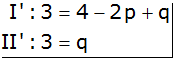Seiten
tauschen |
 |
|
 |
|
 |
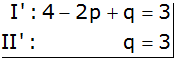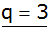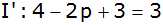q = 3
in I' einsetzen |
 |
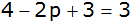Zusammenfassen |
 |
 |
 |
 |
 |
|
 |
|
|
|
|
|
|
 |
|
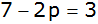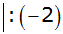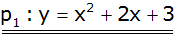3. Vollständige
Wertetabelle: |
|
x |
- 3 |
- 2 |
- 1 |
0 |
1 |
2 |
|
y |
6 |
3 |
2 |
3 |
6 |
11 |
|
|
|
 |
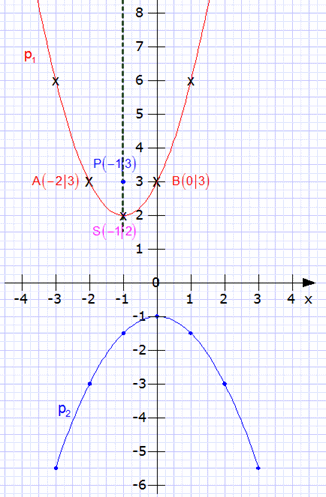
4. Zeichnung der
Parabeln
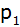und
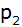im Koordinatensystem: |
|
Wertetabelle von
: |
|
|
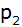x |
- 3 |
- 2 |
- 1 |
0 |
1 |
2 |
|
y |
- 5,5 |
- 3 |
- 1,5 |
- 1 |
- 1,5 |
- 3 |
|
|
|
 |
5.
Rechnerischer Nachweis, dass
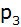weder mit
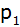noch mit
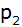einen gemeinsamen Punkt haben: |
 |
|
 |
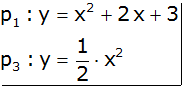Gleichsetzungsverfahren |
 |
 |
 |
 |
 |
|
 |
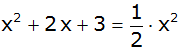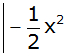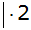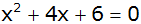Normalform einer
quadratischen Gleichung |
 |
|
 |
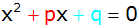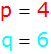p und q bestimmen |
 |
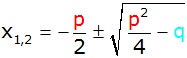Lösungsformel |
 |
|
 |
|
 |
|
 |
|
|
|
 |
 |
|
 |
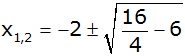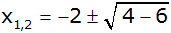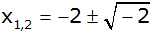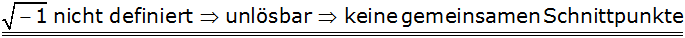