| 1. Berechnung der
Wahrscheinlichkeit mindestens eine "Sechs" zu werfen: |
| Für unsere
Aufgabe gibt es 9 mögliche Ereignisse. |
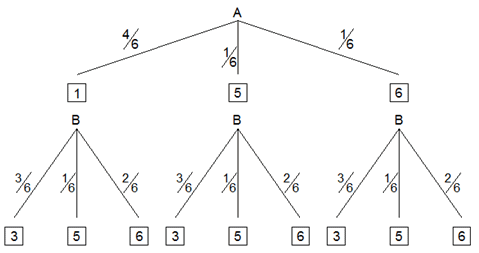
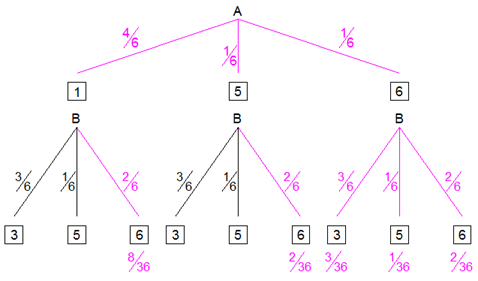
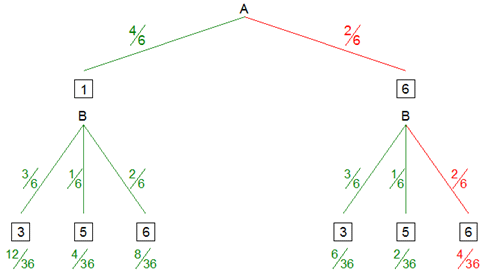
| Das
Experiment wird durch einen
Ereignisbaum
dargestellt. |
| Für den Würfel
A ergeben sich folgende Wahrscheinlichkeiten: |
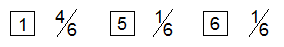 |
| Für den Würfel
B ergeben sich folgende Wahrscheinlichkeiten: |
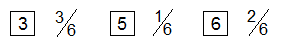 |
|
|
 |
| Für das Ereignis mindestens eine
"Sechs" zu werfen ergeben sich folgende
Wahrscheinlichkeiten: |
|
|
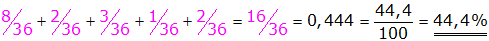 |
|
Antwort: Die
Wahrscheinlichkeit mit den beiden Würfeln mindenstens eine
"Sechs" zu werfen beträgt 44,4 %. |
|
 |
| 2. Berechnung des
Erwartungswertes für das Glückspiel einen Pasch zu werfen: |
| Der
Erwartungswert E berechnet sich nach folgender
Formel: |
|
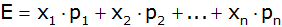 |
|
wobei |
|
 |
|
| Für dieses Glücksspiel gibt es n = 3
mögliche Ereignisse. |
1. man würfelt
  |
2. man würfelt
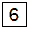 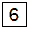 |
3. man würfelt
 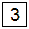 , ,
  , ,
 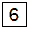 , ,
 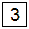 , ,
 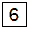 , ,
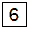 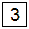 oder
oder
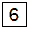  |
|
|
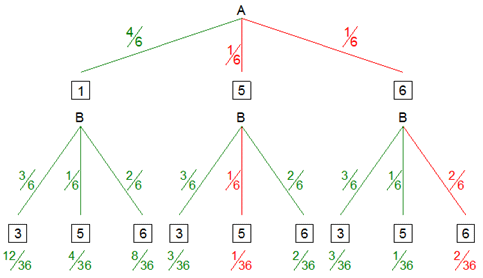
| Es ergeben sich folgende
Wahrscheinlichkeiten: |
|
|
|
|
|
alle anderen
|
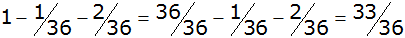 |
|
|
 |
|
|
 |
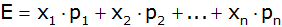 |
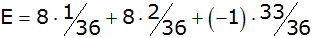 |
 |
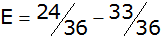 |
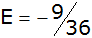 |
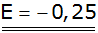 |
|
Antwort: Der Erwartungswert beträgt - 0,25 € |
|
|
3. Berechnung des
Erwartungswertes für das Glückspiels einen Pasch zu werfen
mit verändertem Würfelnetz
 : : |
| Der
Erwartungswert E berechnet sich nach folgender
Formel: |
|
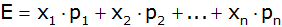 |
|
wobei |
|
 |
|
| Für dieses Glücksspiel gibt es n = 2
mögliche Ereignisse |
1. man würfelt
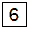 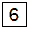 |
2. man würfelt
 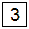 , ,
  , ,
 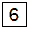 , ,
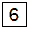 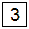 oder
oder
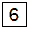  |
|
|
| Es ergeben sich folgende
Wahrscheinlichkeiten: |
|
|
|
alle anderen
|
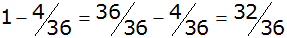 |
|
|
 |
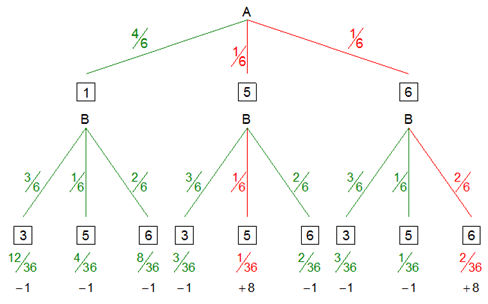
| Es ergeben sich folgende
Gewinnwerte: |
|
|
wirft man einen
6er Pasch, hat man einen Gewinn von 9 €, muß aber
den Kaufpreis von 1 € abziehen |
+
8 |
|
| alle anderen |
wirft man keinen
Pasch, so verliert man den Einsatz von 1 € |
-
1 |
|
|
 |
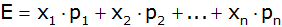 |
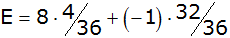 |
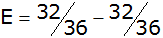 |
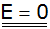 |
|
Antwort: Der Erwartungswert beträgt jetzt 0 €, das heißt,
es wäre für den Veranstalter nicht vorteilhaft. |
|
|





