|
Experiment 1: |
| 12
Sprichworte,
6 Witze
und 2 Kinogutscheine. |
| Mit einem Zug ein
Sprichwort ziehen. |
| Das Experiment
wird durch einen
Ereignisbaum dargestellt. |
|
 |
Da von 20 Glückskeksen 12 mit einem
Sprichwort versehen sind, beträgt die
Wahrscheinlichkeit
mit einem Zug ein Sprichwort zu ziehen,
 . . |
 |
|
Experiment 2:
|
| Das gleichzeitige
Ziehen zweier Glückskekse entspricht dem
Ziehen ohne Zurücklegen. |
| Beim
ersten Ziehen
wird entweder ein
Sprichwort, ein
Witz
oder ein Kinogutschein
gezogen. |
| Beim
zweiten Ziehen
wird wiederum entweder ein
Sprichwort, ein
Witz
oder ein Kinogutschein
gezogen. |
| Das Experiment
wird durch einen
Ereignisbaum dargestellt. |
|
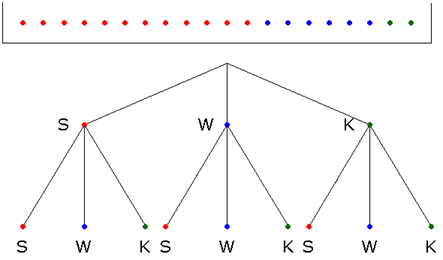 |
Die
Wahrscheinlichkeit
beim ersten Ziehen ein
Sprichwort zu ziehen
beträgt
 . . |
Die
Wahrscheinlichkeit
beim ersten Ziehen einen
Witz zu ziehen beträgt
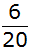 . . |
Die
Wahrscheinlichkeit
beim ersten Ziehen einen
Kinogutschein zu ziehen
beträgt
 . . |
|
 |
| Da der Glückskeks
nach dem ersten Ziehen
nicht wieder in den Korb
zurückgelegt wird, müssen
die Wahrscheinlichkeiten für das
zweite Ziehen
neu bestimmt werden. |
Die
Wahrscheinlichkeit
beim zweiten Ziehen
ein Sprichwort
zu ziehen beträgt für den Fall, dass beim ersten Mal schon
ein Sprichwort
gezogen wurde
 ,
ansonsten ,
ansonsten
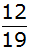 . . |
Die
Wahrscheinlichkeit
beim zweiten Ziehen
einen Witz
zu ziehen beträgt für den Fall, dass beim ersten Mal schon
ein Witz
gezogen wurde
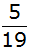 ,
ansonsten ,
ansonsten
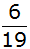 . . |
Die
Wahrscheinlichkeit
beim zweiten Ziehen
einen Kimogutschein
zu ziehen beträgt für den Fall, dass beim ersten Mal schon
ein Kinogutschein
gezogen wurde
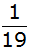 ,
ansonsten ,
ansonsten
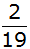 . . |
|
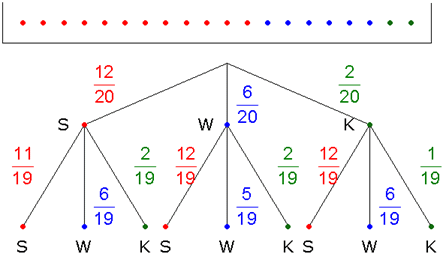 |
| Es ergeben
sich folgende Wahrscheinlichkeiten: |
|
  |
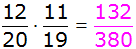 |
|
  |
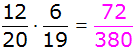 |
|
  |
 |
|
  |
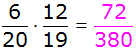 |
|
  |
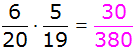 |
|
  |
 |
|
  |
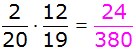 |
|
  |
 |
|
  |
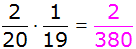 |
|
|
| Berechnung der
Wahrscheinlichkeit, dass zwei Glückskekse unterschiedlicher
Füllung gezogen werden: |
|
|
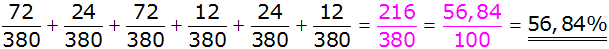 |
| Antwort: Die
Wahrscheinlichkeit, bei dem gleichzeitigen Ziehen zweier
Glückskekse, unterschiedliche Füllung zu erhalten, beträgt
56,84%. |
|
|




