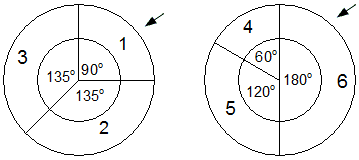
| Das linke
Glücksrad kann beim Drehen
entweder auf 1,
2
oder 3
stehen bleiben. |
| Das rechte
Glücksrad kann entweder auf
4,
5
oder 6
stehen bleiben. |
| Als Summe beider
Glücksräder ergeben sich 5,
6,
7,
8
oder 9. |
Gewinnsituation A:
Summe 8 oder 9
Gewinnsituation B:
alle anderen Summen |
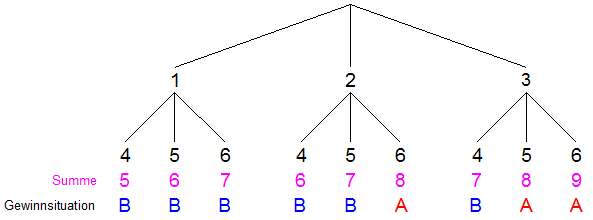
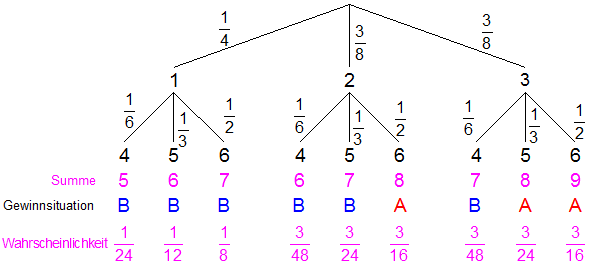
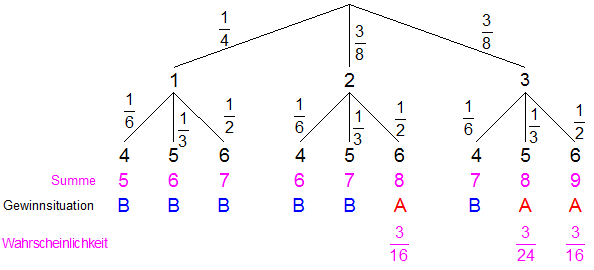
| Das Experiment
wird durch einen
Ereignisbaum dargestellt. |
|
 |
| Die
Wahrscheinlichkeit
dass das linke Glücksrad
auf der 1
stehen bleibt beträgt: |
|

|
| Die
Wahrscheinlichkeit
dass das linke Glücksrad
auf der 2
oder der 3
stehen bleibt beträgt: |
|

|
| Die
Wahrscheinlichkeit
dass das rechte Glücksrad
auf der 4
stehen bleibt beträgt: |
|

|
| Die
Wahrscheinlichkeit
dass das rechte Glücksrad
auf der 5
stehen bleibt beträgt: |
|

|
| Die
Wahrscheinlichkeit
dass das rechte Glücksrad
auf der 6
stehen bleibt beträgt: |
|
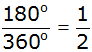
|
|
 |
| Es ergeben
sich folgende Wahrscheinlichkeiten: |
|
B:
1 + 4 = 5 |
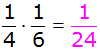 |
|
B:
1 + 5 = 6 |
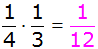 |
|
B:
1 + 6 = 7 |
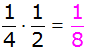 |
|
B:
2 + 4 = 6 |
 |
|
B:
2 + 5 = 7 |
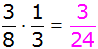 |
|
A:
2 + 6 = 8 |
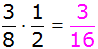 |
|
B:
3 + 4 = 7 |
 |
|
A:
3 + 5 = 8 |
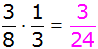 |
|
A:
3 + 6 = 9 |
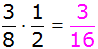 |
|
 |
| Berechnung der
Wahrscheinlichkeit, dass die Summe der erhaltenen Zahlen 8
oder 9 ergibt: |
| |
A: 2 + 6 = 8 |
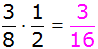 |
|
A: 3 + 5 = 8 |
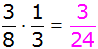 |
|
A: 3 + 6 = 9 |
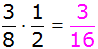 |
|
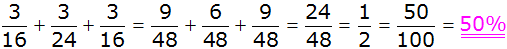 |
|
| Antwort: Die
Wahrscheinlichkeit, dass die Summe der erhaltenen Zahlen 8
oder 9 ergibt, beträgt 50%. D.h. Die Wahrscheinlichkeit für
Situation A oder B sind gleich groß. |
|
 |
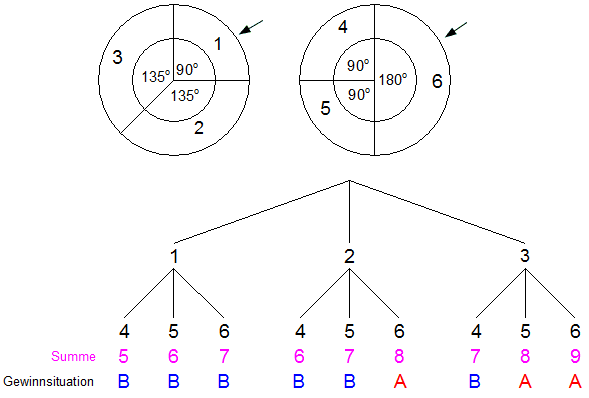
| Das
rechte Glücksrad
wurde so verändert,
dass die Sektoren der Zahlen 4 und 5 jeweils den
Mittelpunktswinkel 90° erhalten. |
| Das linke
Glücksrad kann beim Drehen
entweder auf 1,
2
oder 3
stehen bleiben. |
| Das rechte
Glücksrad kann entweder auf
4,
5
oder 6
stehen bleiben. |
| Als Summe beider
Glücksräder ergeben sich 5,
6,
7,
8
oder 9. |
Gewinnsituation A:
Summe 8 oder 9
Gewinnsituation B:
alle anderen Summen |
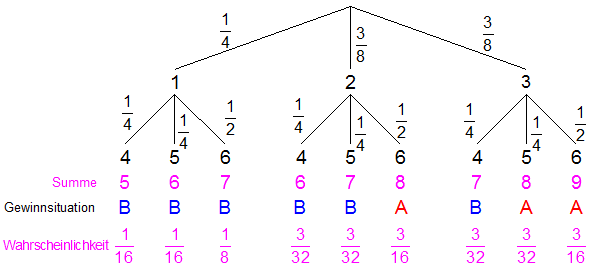
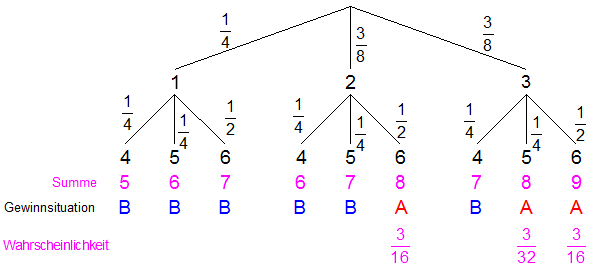
| Das neue
Experiment wird durch einen
Ereignisbaum
dargestellt. |
|
 |
| Die
Wahrscheinlichkeit
dass das linke Glücksrad
auf der 1
stehen bleibt beträgt: |
|

|
| Die
Wahrscheinlichkeit
dass das linke Glücksrad
auf der 2
oder der 3
stehen bleibt beträgt: |
|

|
| Die
Wahrscheinlichkeit
dass das rechte Glücksrad
auf der 4
stehen bleibt beträgt: |
|

|
| Die
Wahrscheinlichkeit
dass das rechte Glücksrad
auf der 5
stehen bleibt beträgt: |
|

|
| Die
Wahrscheinlichkeit
dass das rechte Glücksrad
auf der 6
stehen bleibt beträgt: |
|
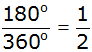
|
|
 |
| Es ergeben
sich folgende Wahrscheinlichkeiten: |
|
B:
1 + 4 = 5 |
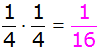 |
|
B:
1 + 5 = 6 |
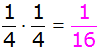 |
|
B:
1 + 6 = 7 |
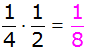 |
|
B:
2 + 4 = 6 |
 |
|
B:
2 + 5 = 7 |
 |
|
A:
2 + 6 = 8 |
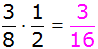 |
|
B:
3 + 4 = 7 |
 |
|
A:
3 + 5 = 8 |
 |
|
A:
3 + 6 = 9 |
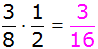 |
|
 |
| Berechnung der
Wahrscheinlichkeit, dass die Summe der erhaltenen Zahlen 8
oder 9 ergibt: |
| |
A: 2 + 6 = 8 |
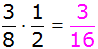 |
|
A: 3 + 5 = 8 |
 |
|
A: 3 + 6 = 9 |
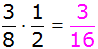 |
|
 |
|
Antwort: Die
Wahrscheinlichkeit, dass die Summe der erhaltenen Zahlen 8
oder 9 ergibt, vermindert sich auf 46,9%. D.h. Die
Wahrscheinlichkeit für Situation B verbessert sich auf
53,1%.
Nach der Veränderung müsste man auf B setzen. |
|
 |








