| Zwei Spielwürfel werden
geworfen. |
|
Das Experiment wird durch einen
Ereignisbaum
dargestellt. |
|
|
|
| Ob die Würfel
gleichzeitig oder nacheinander geworfen werden ist dabei
völlig gleichwertig. |
Die
Wahrscheinlichkeit mit dem ersten Würfel eine entsprechende
Augenzahl zu werfen ist jeweils
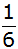 . . |
Die
Wahrscheinlichkeit mit dem zweiten Würfel eine entsprechende
Augenzahl zu werfen ist wiederum
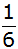 . . |
Es ergeben sich
also insgesamt 36 Ereignisse mit jeweils der
Wahrscheinlichkeit
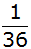 . . |
|
| Die Bedingung
"Augensumme kleiner als 5"
erfüllen 6 Ereignisse. |
|
|
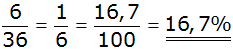
Antwort: Die Wahrscheinlichkeit mit
zwei Würfeln eine Augensumme kleiner als 5 zu werfen beträgt 16,7%. |
| Die Bedingung
"keinen Pasch werfen"
erfüllen 30 Ereignisse. |
|
|
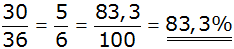
Antwort: Die Wahrscheinlichkeit mit
zwei Würfeln keinen Pasch zu werfen beträgt 83,3%. |
Für die
Wahrscheinlichkeit
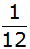 benötigt man genau 3
Ereignisse, die eine
Bedingung erfüllen.
benötigt man genau 3
Ereignisse, die eine
Bedingung erfüllen. |
| Die Bedingung
"Augensumme 4"
erfüllen 3 Ereignisse. |
|
|
|
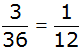
Antwort: Die Wahrscheinlichkeit mit
zwei Würfeln die Augensumme 4 zu werfen beträgt
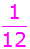 . . |
| Die Bedingung
"Augensumme 10"
erfüllen 3 Ereignisse. |
|
|
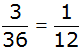
Antwort: Die Wahrscheinlichkeit mit
zwei Würfeln die Augensumme 10 zu werfen beträgt
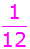 . . |