| In dem Behälter
mit 10 Kugeln,
sind 1 weiß,
4 rot
und 5 blau. |
| Beim
ersten Ziehen
wird entweder eine weiße,
eine rote
oder eine blaue
Kugel gezogen. |
| Da
ohne Zurücklegen
gezogen wird, wird beim
zweiten Ziehen im Falle,
dass zuerst eine weiße
Kugel gezogen wurde,
entweder eine rote
oder eine blaue Kugel
gezogen. Wurde jedoch zuerst eine
rote
oder blaue Kugel
gezogen, wird wiederum entweder eine
weiße,
eine rote
oder eine blaue
Kugel gezogen. |
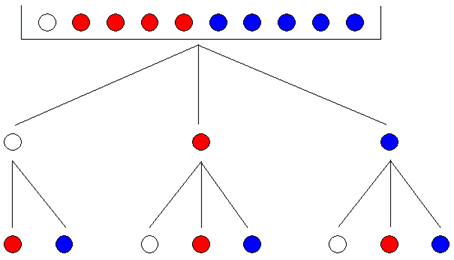
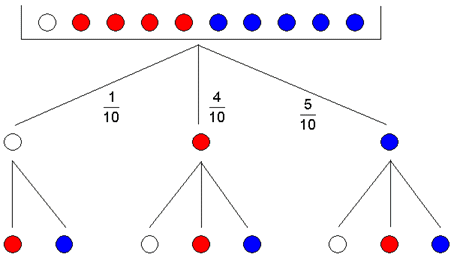
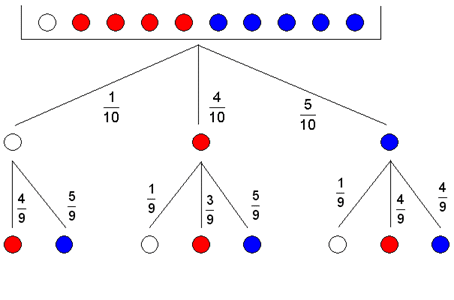
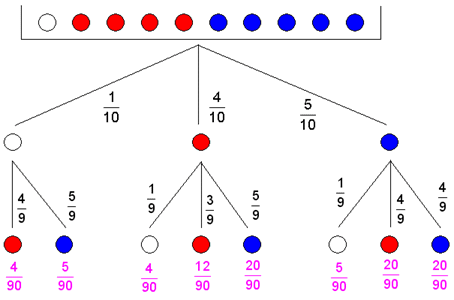
| Das Experiment
wird durch einen
Ereignisbaum dargestellt. |
|
 |
Die
Wahrscheinlichkeit
beim ersten Ziehen eine
weiße Kugel zu ziehen
beträgt
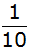 . . |
Die
Wahrscheinlichkeit
beim ersten Ziehen eine
rote Kugel zu ziehen
beträgt
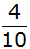 . . |
Die
Wahrscheinlichkeit
beim ersten Ziehen eine
blaue Kugel zu ziehen
beträgt
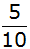 . . |
|
 |
| Da die Kugel nach
dem ersten Ziehen
nicht wieder in den Behälter
zurückgelegt
wird, müssen die Wahrscheinlichkeiten für das
zweite Ziehen
neu bestimmt werden. |
Die
Wahrscheinlichkeit
beim zweiten Ziehen
eine weiße Kugel
zu Ziehen beträgt für den Fall, dass beim ersten Mal schon
eine weiße Kugel
gezogen wurde
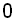 ,
ansonsten ,
ansonsten
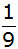 . . |
Die
Wahrscheinlichkeit
beim zweiten Ziehen
eine rote Kugel
zu Ziehen beträgt für den Fall, dass beim ersten Mal schon
eine rote Kugel
gezogen wurde
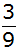 ,
ansonsten ,
ansonsten
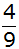 . . |
Die
Wahrscheinlichkeit
beim zweiten Ziehen
eine blaue Kugel
zu Ziehen beträgt für den Fall, dass beim ersten Mal schon
eine blaue Kugel
gezogen wurde
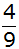 ,
ansonsten ,
ansonsten
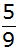 . . |
|
 |
| Es ergeben
sich folgende Wahrscheinlichkeiten: |
|
  |
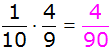 |
|
  |
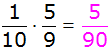 |
|
  |
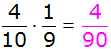 |
|
  |
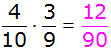 |
|
  |
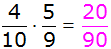 |
|
  |
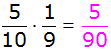 |
|
  |
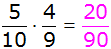 |
|
  |
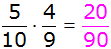 |
|
 |
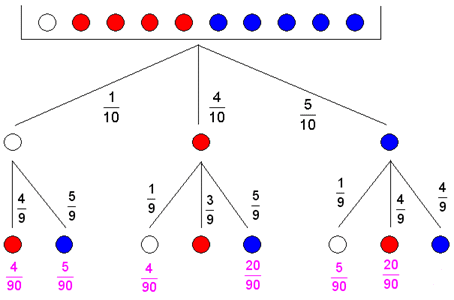
| Berechnung der
Wahrscheinlichkeit, dass zwei verschiedenfarbige Kugeln
gezogen werden: |
|
|
| Antwort: Die
Wahrscheinlichkeit, dass zwei verschiedenfarbige Kugeln
gezogen werden beträgt 64,4%. |
|
 |
| Berechnung der
Wahrscheinlichkeit, dass höchstens eine der gezogenen Kugeln
rot ist: |
Alle
Zugkombinationen sind möglich außer
  . . |
|
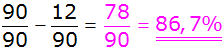 |
|
|
| Antwort: Die
Wahrscheinlichkeit, dass höchstens eine der gezogenen Kugeln
rot ist, beträgt 86,7%. |
|
|