| Das Glücksrad kann
beim ersten Drehen entweder
auf 6, 10 oder 20 stehen
bleiben. |
| Beim zweiten
Drehen kann es wiederum auf 6, 10 oder 20
stehen bleiben. |
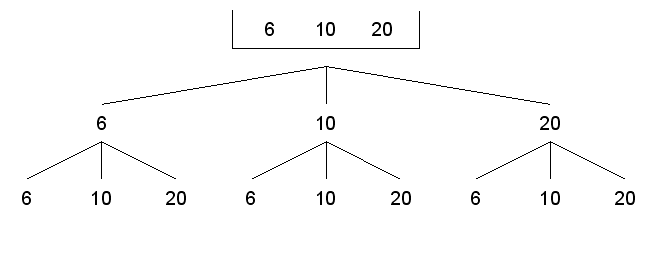
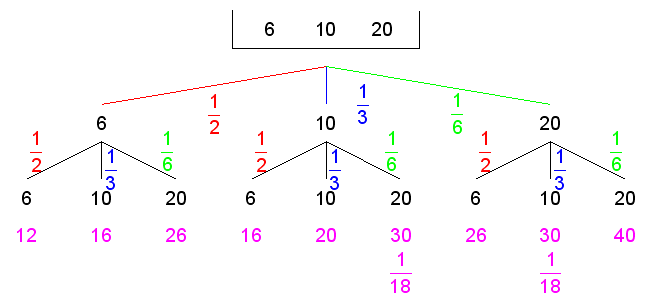
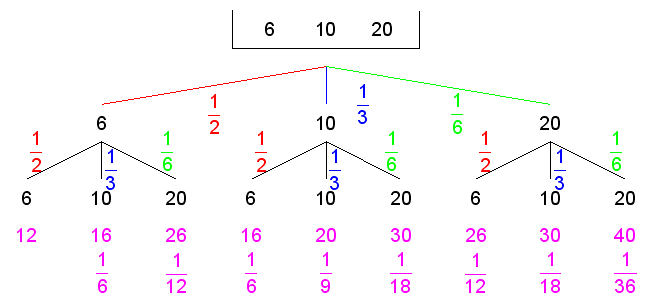
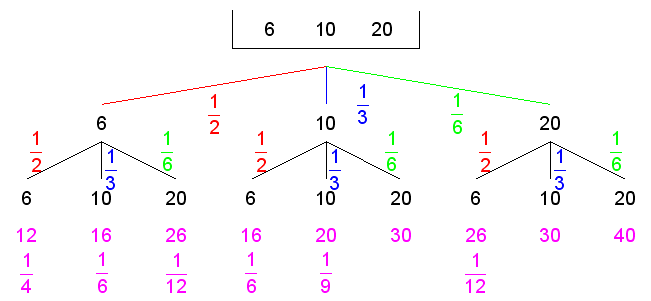
| Das Experiment wird
durch einen Ereignisbaum dargestellt. |
|
 |
| Die Wahrscheinlichkeit dass
das Glücksrad beim ersten Drehen auf der 6 stehen
bleibt beträgt: |
|
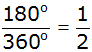
|
| Die Wahrscheinlichkeit dass
das Glücksrad beim ersten Drehen auf der 10 stehen
bleibt beträgt: |
|
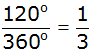
|
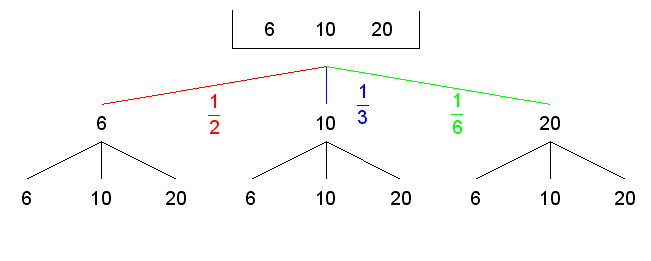
| Die Wahrscheinlichkeit dass
das Glücksrad beim ersten Drehen auf der 20 stehen
bleibt beträgt: |
|

|
|
 |
|
Die Wahrscheinlichkeiten beim zweiten Drehen sind dieselben wie beim
ersten Drehen. |
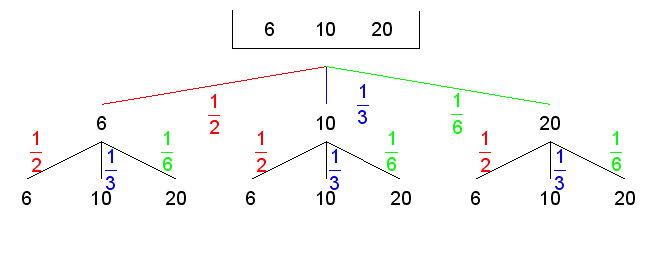 |
| Es
ergeben sich folgende Wahrscheinlichkeiten: |
| 6 + 6 = 12 |
 |
| 6 + 10 = 16 |
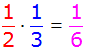 |
| 6 + 20 = 26 |
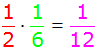 |
| 10 + 6 = 16 |
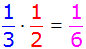 |
| 10 + 10 = 20 |
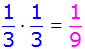 |
| 10 + 20 = 30 |
 |
| 20 + 6 = 26 |
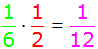 |
| 20 + 10 = 30 |
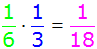 |
| 20 + 20 = 40 |
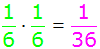 |
|
 |
|
1. Berechnung der Wahrscheinlichkeit, dass die Summe der
erhaltenen Zahlen genau 30 ergibt: |
| 10 + 20
= 30 |
 |
| 20 + 10
= 30 |
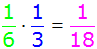 |
| |
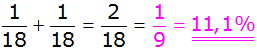 |
|
|
Antwort: Die
Wahrscheinlichkeit, dass die Summe der erhaltenen Zahlen
genau 30 ergibt, beträgt 11,1%. |
|
 |
|
2. Berechnung der Wahrscheinlichkeit, dass die Summe der
erhaltenen Zahlen größer als 12 ist: |
| Da
alle Ereignisse außer das folgende zutreffen |
| 6 + 6 = 12 |
 |
beträgt die Wahrscheinlichkeit 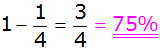 |
|
|
Antwort: Die
Wahrscheinlichkeit, dass die Summe der erhaltenen Zahlen
größer als 12 ist, beträgt 75%. |
|
 |
|
3. Berechnung der Wahrscheinlichkeit, dass die Summe der
erhaltenen Zahlen kleiner als 30 ist: |
6 + 6 = 12 |
 |
| 6 + 10 = 16 |
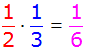 |
|
| 6 + 20 = 26 |
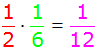 |
|
| 10 + 6 = 16 |
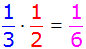 |
|
| 10 + 10
= 20 |
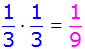 |
|
| 20 + 6 = 26 |
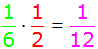 |
|
| |
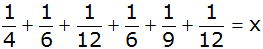 |
| |
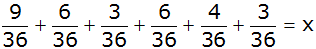 |
| |
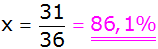 |
|
|
Antwort: Die
Wahrscheinlichkeit, dass die Summe der erhaltenen Zahlen
kleiner als 30 ist, beträgt 86,1%. |
|
 |