| In dem Behälter mit 10
Kugeln, sind 5 blau, 3
weiß und 2 rot. |
| Beim ersten
Ziehen wird entweder eine blaue,
eine weiße oder eine rote Kugel
gezogen. |
| Beim zweiten
Ziehen wird wiederum entweder eine blaue,
eine weiße oder eine rote Kugel
gezogen. |
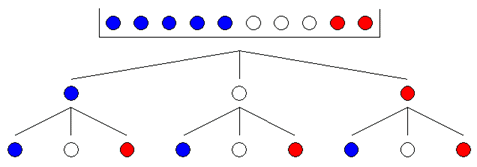
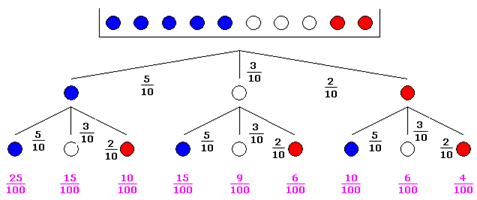
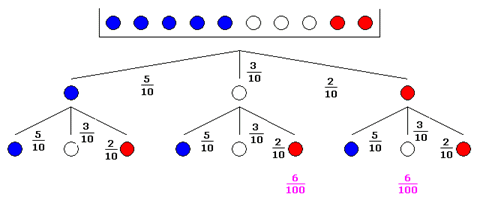
| Das Experiment wird
durch einen Ereignisbaum dargestellt. |
|
 |
Die Wahrscheinlichkeit, beim
ersten Ziehen eine blaue Kugel zu
ziehen, beträgt 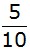 . . |
Die Wahrscheinlichkeit, beim
ersten Ziehen eine weiße Kugel zu
ziehen, beträgt 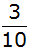 . . |
Die Wahrscheinlichkeit, beim
ersten Ziehen eine rote Kugel zu
ziehen, beträgt 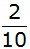 . . |
|
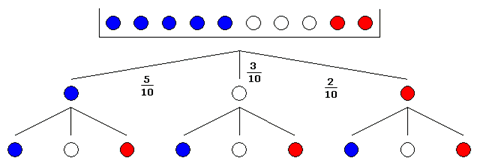 |
| Da die Kugel nach dem
ersten Ziehen wieder in den Behälter zurückgelegt wird,
sind die Wahrscheinlichkeiten für das Ziehen dieselben wie
beim ersten Ziehen. |
Die Wahrscheinlichkeit, beim
zweiten Ziehen eine blaue Kugel zu
ziehen, beträgt 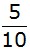 . . |
Die Wahrscheinlichkeit, beim
zweiten Ziehen eine weiße Kugel zu
ziehen, beträgt 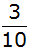 . . |
Die Wahrscheinlichkeit, beim
zweiten Ziehen eine rote Kugel zu
ziehen, beträgt 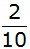 . . |
|
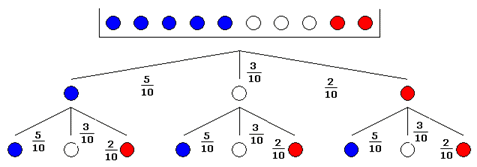 |
| Es
ergeben sich folgende Wahrscheinlichkeiten: |
| |
  |
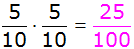 |
| |
  |
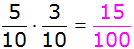 |
| |
  |
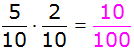 |
| |
  |
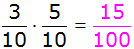 |
| |
  |
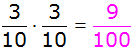 |
| |
  |
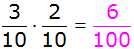 |
| |
  |
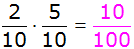 |
| |
  |
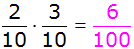 |
| |
  |
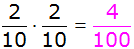 |
|
 |
| 1.
Berechnung der Wahrscheinlichkeit, dass zwei gleichfarbige
Kugeln gezogen werden: |
| |
  |
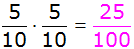 |
| |
  |
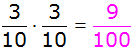 |
| |
  |
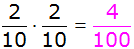 |
| |
|
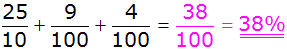 |
| |
Antwort: Die
Wahrscheinlichkeit, dass zwei gleichfarbige Kugeln gezogen
werden beträgt 38%. |
|
 |
| 2.
Berechnung der Wahrscheinlichkeit, dass von den beiden
gezogenen Kugeln eine rot und eine weiß ist: |
| |
  |
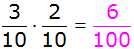 |
| |
  |
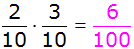 |
| |
|
 |
| |
Antwort: Die
Wahrscheinlichkeit, dass von den beiden gezogenen Kugeln
eine rot und eine weiß ist beträgt 12%. |
|
 |