1. Berechnung
des Scheitelpunktes
der Parabel
 : |
 |
Punktkoordinaten einsetzen:
 |
 |
|
 |
|
 |
Seiten
tauschen |
 |
 |
 |
|
 |
|
 |
Quadratische Ergänzung |
 |
1.
binomische Formel |
 |
Zusammenfassen |
 |
|
 |
|
 |
Scheitelgleichung |
 |
|
 |
|
|
|
 |
2. Zeichnung der Parabeln
und
in das Koordinatensystem: |
Die Parabel
ist nach oben geöffnet und läßt sich durch Anlegen
der Schablone an den Scheitelpunkt
zeichnen. |
Die Parabel
ist nach unten geöffnet und läßt sich durch Anlegen
der Schablone an den Scheitelpunkt
zeichnen. |
|
|
 |
3. Berechnung der Koordinaten
der beiden Schnittpunkte
und
 : |
 |
Gleichsetzungsverfahren |
 |
 |
 |
 |
 |
Quadratische Gleichung in der Normalform |
 |
|
 |
p und
q bestimmen |
 |
|
 |
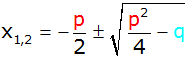Lösungsformel |
 |
|
 |
|
 |
|
 |
|
 |
|
 |
x1 = 1 in II einsetzen |
 |
|
 |
|
 |
|
 |
x2 = - 2 in II einsetzen |
 |
|
 |
|
|
|
 |
4. Berechnung der
Funktionsgleichung der Geraden
durch
und
: |
 |
Allgemeine
Geradengleichung |
 |
Punktkoordinaten einsetzen:
Punktkoordinaten einsetzen:
 |
 |
Seiten
tauschen |
 |
 |
 |
Additionsverfahren |
 |
 |
 |
|
 |
b = - 2 in
I einsetzen |
 |
Seiten
tauschen |
 |
 |
 |
|
 |
|
|
|
 |
