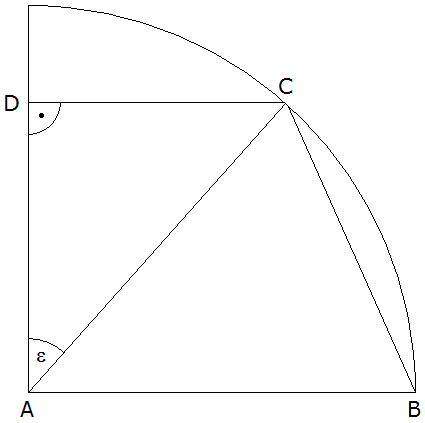
Im nebenstehenden rechtwinkligen Trapez ABCD liegen die Punkte B und C auf einem Viertelkreis um A mit dem Radius .
Bewegt sich Punkt C auf der Kreislinie, so entstehen im Viertelkreis jeweils andere rechtwinklige Trapeze.

Geben Sie die Länge von in Abhängigkeit von an.

Tabellieren Sie die Werte für in Abhängigkeit von in Schritten von im Intervall 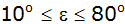und stellen Sie diese Abhängigkeit in einem rechtwinkligen Koordinatensystem dar.
Entnehmen Sie dem Schaubild (deutliche Kennzeichnung) den Wert von für 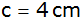. Ermitteln Sie den genauen Wert von durch Rechnung und bestimmen Sie mit diesem Wert den Flächeninhalt des Trapezes.