|
|
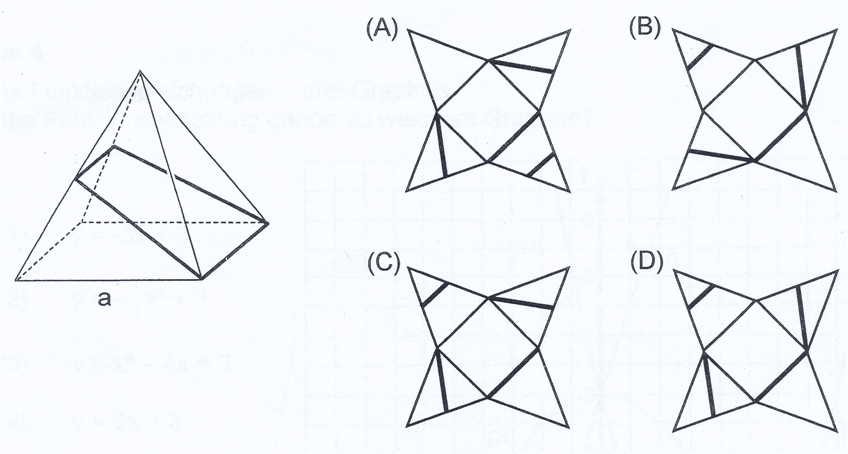
| Auf der Mantelfläche
der quadratischen Pyramide ist ein Streckenzug eingezeichnet. |
| Auf welchem der vier
abgebildeten Netze wird der Streckenzug richtig dargestellt? |
 |
|
|
Aufgabe A1/1b: |
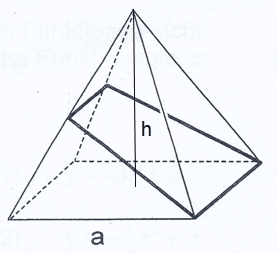
Die Grundkante a der
quadratischen Pyramide ist 5 cm lang.
Die
Körperhöhe h beträgt 6 cm.
Berechnen Sie das
Volumen der quadratischen Pyramide. |
|
 |
|
|
|
|
|
|
|
In einem Behälter liegen
gelbe, rote und blaue Kugeln.
Insgesamt sind es sechs
Stück.
Kim zieht ohne
hinzuschauen zwei Kugeln gleichzeitig.
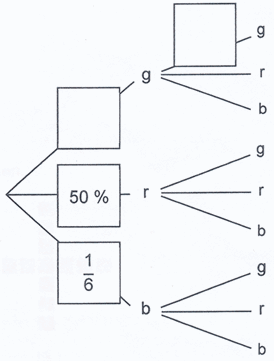
Im Baumdiagramm sind zwei
Wahrscheinlichkeiten angegeben.
Ergänzen Sie in den beiden
leeren Feldern die Wahrscheinlichkeitsangaben. |
 |
|
|
|
|
|
|
In einem Behälter liegen
gelbe, rote und blaue Kugeln.
Insgesamt sind es sechs
Stück.
Kim zieht ohne
hinzuschauen zwei Kugeln gleichzeitig.
Wie groß ist die
Wahrscheinlichkeit, dass Kim zwei rote Kugeln zieht? |
 |
|
|
|
|
|
Aufgabe A1/4a: |
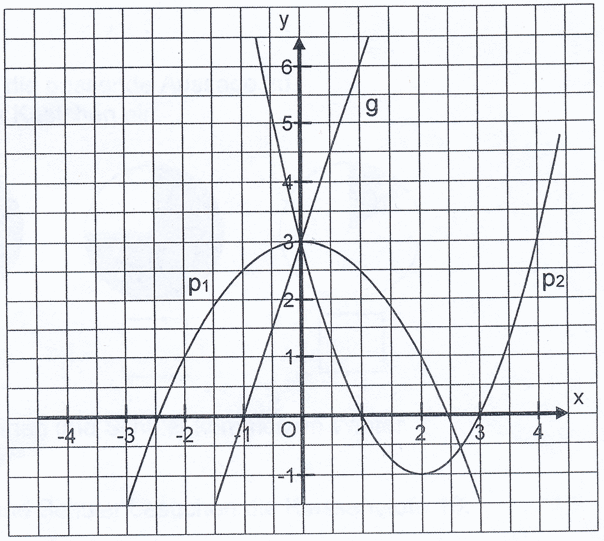
Sechs
Funktionsgleichungen - drei Graphen.
Welche
Funktionsgleichung gehört zu welchem Graphen? |
| |
 |
|
|
|
|
 |
|
|
|
Aufgabe A1/4b: |
Die Gerade
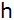 hat die Funktionsgleichung
hat die Funktionsgleichung
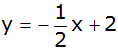 . .
Zeichnen Sie die Gerade in das abgebildete
Koordinatensystem. |
|
|
 |
|
|
|
|
|
|
|
Johannes legt drei Muster mit quadratischen Kärtchen. |
|
|
|
Er behauptet: "Das 10. Muster besteht aus 43 Kärtchen." |
|
Hat Johannes Recht? |
|
Begründen Sie Ihre Aussage. |
|
|
|
|
|
Ordnen Sie jedem Kreisdiagramm die passende Aussage zu.
Tragen Sie den Buchstaben in das Kästchen ein. |
|
|
| (A) |
Drei Viertel der Schülerinnen und Schüler kommen
im Winter mit dem Bus zur Schule.
|
| (B) |
15% der Schülerinnen und Schüler besuchen die
Klassenstufe 10.
|
| (C) |
200 von 300 Schülerinnen und Schüler haben
Geschwister.
|
| (D) |
40% der Schülerinnen und Schüler fahren im
Sommer mit dem Fahrrad zur Schule.
|
|
|
|
|
|
Pflichtaufgaben |
|
Aufgabe A2/1: |
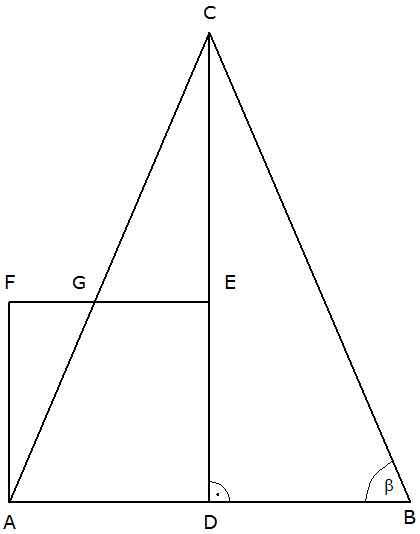
| Das gleichschenklige Dreieck ABC und
das Quadrat ADEF überdecken sich teilweise. |
| Es gilt: |
|
|
| Berechnen Sie den Umfang des
Dreiecks GEC. |
|
 |
|
|
|
Aufgabe A2/2: |
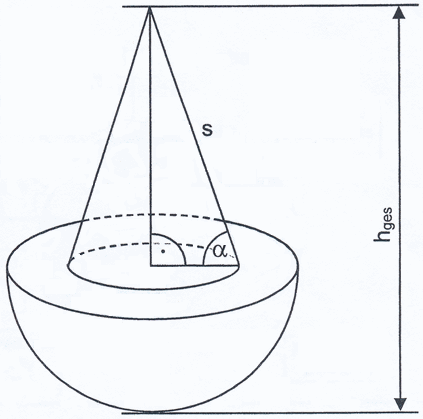
| Ein Kunstwerk setzt sich aus einer
Halbkugel und einem Kegel zusammen. |
| Es gilt: |
|
|
| |
- Berechnen Sie den Oberflächeninhalt des
zusammengesetzten Körpers.
|
Diese Kunstwerk soll mit Farbe
angestrichen werden.
Eine 1-Liter-Farbdose reicht für 10
m2. |
- Wie viele Dosen müssen gekauft werden?
|
|
 |
|
|
|
Aufgabe A2/3: |
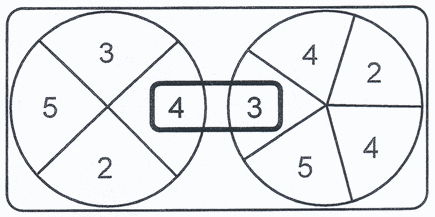
| Die beiden Glücksräder werden
gedreht. |
| Wenn sie stehen bleiben, erkennt man
im Sichtfenster eine zweistellige Zahl. |
| Die Abbildung zeigt die Zahl 43. |
| |
| Mit welcher Wahrscheinlichkeit ist
im Sichtfenster |
- eine Zahl mit zwei gleichen Ziffern zu sehen?
|
- eine durch 12 teilbare Zahl zu sehen?
|
- höchstens einmal die Ziffer 4 zu sehen?
|
|
 |
|
|
|
Aufgabe A2/4: |
|
Immer mehr Menschen kaufen im Internet ein. Die Grafik
zeigt die Umsatzentwicklung des Online-handels in
Deutschland.
|
- Um wie viel Prozent ist der
Umsatz des Online-handels von 2016 bis 2019 insgesamt
gestiegen?
|
| Das Kreisdiagramm zeigt
die Umsatzanteile verschiedener Bereiche am Gesamtumsatz des
Onlinehandels im Jahr 2017. |
- Wie hoch war der Umsatz (in
Euro) für den Bereich "Freizeit und Hobby"?
|
| Laut einer Untersuchung
entfielen im Jahr 2017 allein 53,0% des Bereichs
"Elektronik" auf den Onlinehandel mit Smartphones. |
- Wie viele Euro wurden nach
dieser Untersuchung im Onlinehandel für Smartphones
ausgegeben?
|
|
 |
|
|
|
|
Die Parabel
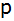 hat die
Funktionsgleichung hat die
Funktionsgleichung
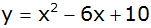 . . |
Eine Gerade
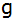 besitzt
die Steigung besitzt
die Steigung
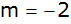 . . |
Sie geht durch den Scheitelpunkt
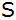 der
Parabel der
Parabel
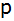 . . |
- Berechnen Sie die Koordinaten des zweiten
Schnittpunktes
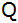 der
Parabel der
Parabel
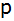 mit
der Geraden mit
der Geraden
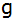 . .
|
Die Gerade
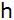 verläuft senkrecht zur Geraden
verläuft senkrecht zur Geraden
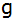 und
geht durch den Punkt und
geht durch den Punkt
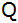 . . |
- Berechnen Sie die Funktionsgleichung der Geraden
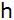 . .
|
|
|
|
Aufgabe A2/6: |
| Im Rahmen einer Umfrage wurden 25
Männer und 25 Frauen getrennt voneinander befragt, wie viele
Stunden sie pro Woche lesen. |
| Die Ergebnisse dieser Befragungen
sind in denn beiden Boxplots dargestellt. |
|
|
| Außerdem sind die Ergebnisse der
Befragungen in den beiden Säulendiagrammen abgebildet, wobei
das Diagramm (2) unvollständig ist. |
- Welcher Boxplot gehört zu
Diagramm (1)? Begründen Sie mit Hilfe der Kennwerte.
|
|
|
| Der andere Boxplot gehört zu
Diagramm (2). Hier fehlen Säulen von 8 bis 16 Stunden
Lesezeit. |
- Ergänzen Sie mögliche Säulen im
Diagramm (2) für die Werte von 8 bis 16 Stunden Lesezeit
mit Hilfe des zugehörigen Boxplots.
|
| Finn behauptet: "Über die Hälfte der
Männer liest 7 Stunden oder mehr pro Woche." |
- Hat Finn Recht? Begründen Sie.
|
|
|
|
|
Wahlaufgaben |
|
Aufgabe B/1a: |
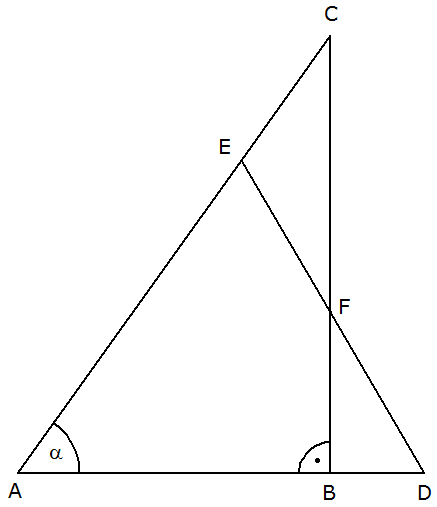
| Gegeben sind das rechtwinklige
Dreieck ABC und das gleichschenklige Dreieck ADE |
| Es gilt: |
|
|
- Berechnen Sie die Länge von
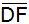 . .
|
- Berechnen Sie den Umfang des Vierecks ABFE.
|
|
 |
|
|
|
Aufgabe B/1b: |
Die Punkte
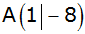 und
und
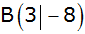 liegen auf einer nach oben geöffneten verschobenen
Normalparabel
liegen auf einer nach oben geöffneten verschobenen
Normalparabel
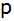 . . |
|
- Geben Sie die Funktionsgleichung
der Parabel
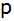 in
der Normalform in
der Normalform
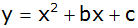 an. an.
|
Die Schnittpunkte der Parabel 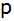 mit der x-Achse und die
Punkte mit der x-Achse und die
Punkte 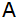 und
und
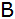 bilden ein Viereck.
bilden ein Viereck. |
- Berechnen Sie den Flächeninhalt
dieses Vierecks.
|
Die Geraden
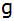 und
und
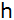 verlaufen jeweils auf den Diagonalen des Vierecks.
verlaufen jeweils auf den Diagonalen des Vierecks.
Sie schneiden sich im Punkt
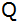 . . |
- Berechnen Sie die Koordinaten
des Schnittpunktes
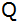 . .
|
|
|
|
|
Aufgabe B/2a: |
Der Punkt
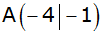 liegt auf der Parabel
liegt auf der Parabel
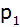 mit der Funktionsgleichung
mit der Funktionsgleichung
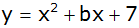 . . |
Die Gerade
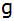 schneidet die Parabel
schneidet die Parabel
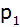 im Punkt
im Punkt
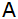 und im Scheitelpunkt
und im Scheitelpunkt
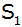 . . |
|
- Berechnen Sie die
Funktionsgleichungen der Parabel
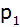 und
der Geraden und
der Geraden
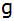 . .
|
Durch Spiegelung des Scheitelpunktes
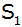 an der
y-Achse entsteht der Punkt an der
y-Achse entsteht der Punkt
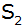 . . |
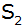 ist der
Scheitelpunkt einer nach oben geöffneten verschobenen
Normalparabel ist der
Scheitelpunkt einer nach oben geöffneten verschobenen
Normalparabel
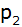 . . |
- Geben Sie die Funktionsgleichung
von
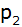 in der Form
in der Form
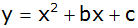 an. an.
|
Der Schnittpunkt der Geraden
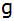 mit der y-Achse ist der Scheitelpunkt
mit der y-Achse ist der Scheitelpunkt
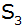 der
Parabel der
Parabel
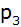 .
Die Parabel .
Die Parabel
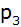
der Form
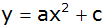 geht außerdem durch die Scheitelpunkte
geht außerdem durch die Scheitelpunkte
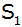 und und
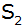 . . |
- Berechnen Sie die
Funktionsgleichung der Parabel
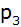 . .
|
|
|
|
|
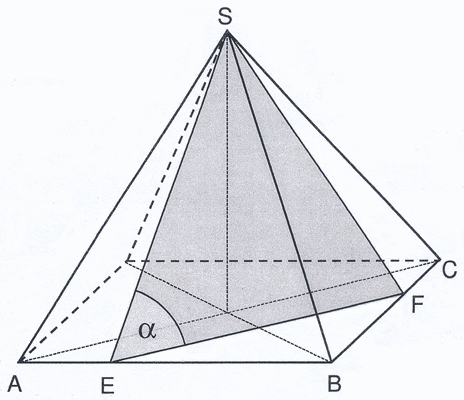
Aufgabe B/2b: |
| In einer quadratischen Pyramide
liegt das gleichschenklige Dreieck EFS. |
| Es gilt: |
|
|
- Berechnen Sie den Flächeninhalt des Dreiecks EFS.
|
- Berechnen Sie das Volumen der quadratischen
Pyramide.
|
|
 |
|
|
|
Aufgabe B/3a: |
| Zehn gleich große Karten sind mit
vier verschiedenen Symbolen (Handball, Radfahren, Laufen,
Fußball) bedruckt. |
| Sie sind nach den vier Symbolen in
Stapeln sortiert (siehe Abbildung). |
| Die Karten werden gemischt und
verdeckt auf den Tisch gelegt. |
| Sie werden für ein Glücksspiel
eingesetzt. |
| Dabei werden zwei Karten
gleichzeitig gezogen. |
| Für das Spiel wird der abgebildete
Gewinnplan geprüft. |
- Berechnen Sie den
Erwartungswert.
|
| Der Veranstalter möchte langfristig
pro Spiel einen Erlös von 0,50 € erzielen. |
- Wie hoch muss dann der Gewinn
für "
 "
sein, wenn alles andere unverändert bleibt? "
sein, wenn alles andere unverändert bleibt?
|
|
 |
|
|
|
Aufgabe B/3b: |
|
Die Flugbahn eines Speers ist nahezu parabelförmig. |
Der Abwurfpunkt
 liegt
1,80 m über der Abwurflinie. liegt
1,80 m über der Abwurflinie. |
Der Speer
erreicht nach 20 m, in horizontaler Richtung von der
Abwurflinie gemessen, seine maximale
Höhe von 9,80 m. |
 |
- Berechnen Sie eine mögliche Funktionsgleichung der
Flugkurve des Speers.
- Wie weit fliegt der Speer?
|
Ein zweiter
Wurfversuch kann mit der Funktionsgleichung
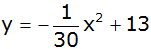 beschrieben werden.
beschrieben werden.
Die Wurfweite beträgt 38,15 m. |
- Geben Sie die Höhe dieses Abwurfpunktes an.
|
|
|
|
|
|
|
|
|