Home Geschichte Informatik Lernmaterial Linkliste Mathematik Smartphone ARS LB
2010 Übersicht
nach oben
Pflichtaufgaben
Aufgabe P1:
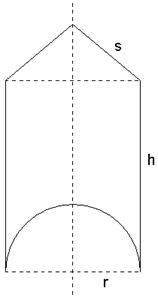
Ein zusammengesetzter Körper besteht aus einem Zylinder mit aufgesetztem Kegel.
Aus diesem Körper wird eine Halbkugel herausgearbeitet (siehe Achsenschnitt).
Es gilt:
Berechnen Sie das Volumen des Restkörpers.
4 P
Aufgabe P2:
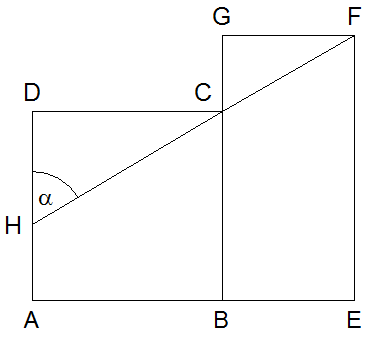
Ein Quadrat und ein Rechteck haben die Punkte B und C gemeinsam.
Es gilt:
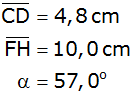Berechnen Sie den Umfang des Vierecks BEFC.
4,5 P
Aufgabe P3:
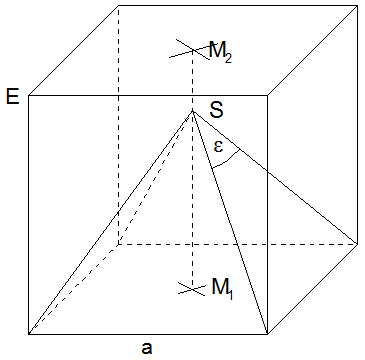
Das Schrägbild zeigt eine Pyramide in einem Würfel.
Es gilt:
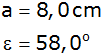Wie groß ist das Volumen der Pyramide?
Berechnen Sie die Länge .
4,5 P
Aufgabe P4:

Lösen Sie das Gleichungssystem:
3 P
Aufgabe P5:
Die nach unten geöffnete Parabel hat die Gleichung .  
Zeichnen Sie die Parabel in ein Koordinatensystem.  
    
Die Gerade g hat die Steigung 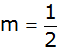und schneidet die y-Achse im Punkt .  
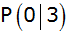Berechnen Sie die Koordinaten der Schnittpunkte von p und g.
3,5 P
Aufgabe P6:
In einem Behälter befinden sich  drei blaue und drei rote Kugeln.

Viola führt zwei Zufallsexperimente durch:

Experiment 1: Sie zieht zwei Kugeln mit Zurücklegen
Experiment 2: Sie zieht zwei Kugeln ohne Zurücklegen
 
Sie vermutet: "In beiden Experimenten ist die Wahrscheinlichkeit, zwei verschiedenfarbige Kugeln zu ziehen, fünfzig Prozent."
 
Überprüfen Sie diese Vermutung.
3,5 P
Aufgabe P7:
Die Klasse 10c wurde über die Anzahl der im letzten Monat versandten SMS befragt.
Die Tabelle zeigt die Angaben von 12 Jungen und von 15 Mädchen:

Jungen

 5 0 39 21 77 14 46 25 128 24 35 66      

Mädchen

 37 29 67 36 10 47 34 177 56 116 28 51 80 0 132
Um wieviel Prozent liegt das arithmetische Mittel der versandten SMS der 15 Mädchen über dem der 12 Jungen?

Geben Sie die Zentralwerte der beiden Datenreihen an.

Florian (20 SMS), Eva (15 SMS) und Laura (170 SMS) können ihre Werte erst nachträglich mitteilen.

Welchen Einfluss hat dies auf die bereits ermittelten Zentralwerte?
Begründen Sie Ihre Aussage.
3,5 P
Aufgabe P8:
 
Die Grafik veranschaulicht die Zuschauerentwicklung eines Fußballvereins von der Spielzeit 03/04 bis zur Spielzeit 08/09.
Zwischen welchen Spielzeiten liegt die größte Steigerung vor; wie viel Prozent beträgt sie? (Entnehmen Sie der Zeichnung die notwendigen Werte so genau wie möglich).
Um die Zuschauerzahl für 09/10 vorhersagen zu können, wird die prozentuale Veränderung zwischen 07/08 und 08/09 ermittelt.
Diese prozentuale Veränderung verwendet der Verein für die Prognose.
 
Mit welcher Zuschauerzahl kann er für 09/10 planen?
3,5 P
Wahlaufgaben
Aufgabe W1a:
Im Quadrat ABCD gilt:
Berechnen Sie den Umfang des Vierecks DEFC.
6 P
Aufgabe W1b:
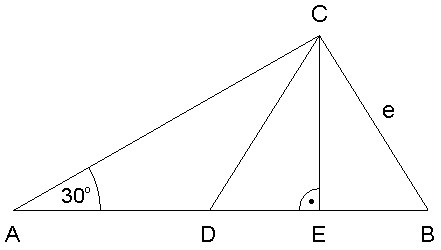
Im Dreieck ABC liegt das gleichseitige Dreieck DBC.

Der Mittelpunkt der Strecke 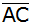wird mit M bezeichnet.

Weisen Sie ohne Verwendung gerundeter Werte nach, dass gilt:
4 P
Aufgabe W2a:
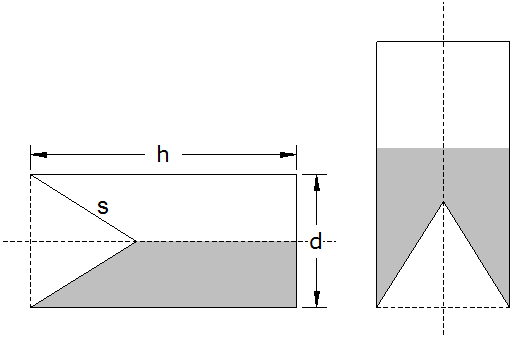
Ein zylinderförmiger Behälter hat eine kegelförmige Vertiefung.
Er liegt waagrecht und ist zur Hälfte mit Wasser gefüllt.

Die Maße sind:
Der Behälter wird senkrecht aufgestellt (siehe rechte Skizze).

Wie hoch steht das Wasser im aufgestellten Behälter?
6 P
Aufgabe W2b:
Aus einem rechteckigen Stück Papier wird der Mantel einer sechsseitigen Pyramide gefertigt.

Der Punkt M ist Mittelpunkt der Seitenkante.
Bestimmen Sie die Länge der Strecke 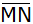in der Pyramide.
4 P
Aufgabe W3a:
Im Schaubild sind die Geraden  und  dargestellt.

Entnehmen Sie zur Bestimmung ihrer Gleichungen geeignete Werte.

Berechnen Sie die Koordinaten des Schnittpunktes von  und .

Die Punkte und liegen auf einer nach oben geöffneten Normalparabel.

Berechnen Sie die Koordinaten des Scheitelpunktes der Parabel.
6 P
Aufgabe W3b:
Gegeben sind die beiden Parabeln:

Die beiden Parabeln schneiden sich in den Punkten und .
Die Punkte und bilden zusammen mit den Scheitelpunkten und das Viereck .

Berechnen Sie seinen Flächeninhalt.

Begründen Sie, weshalb das Viereck ein Drachenviereck ist.
4 P
Aufgabe W4a:

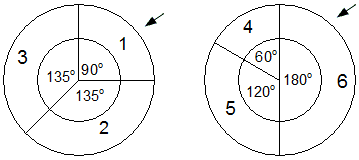
Die beiden Glücksräder werden gedreht.
Die Ergebnisse beider Glücksräder werden addiert.

Es werden zwei Gewinnsituationen angeboten:
Gewinnsituation A: "Summe 8 oder 9" Gewinnsituation B: "alle anderen Summen"

Für welche würden Sie sich entscheiden?

Anschließend wird das rechte Glücksrad so verändert, dass die Sektoren der Zahlen 4 und 5
jeweils den Mittelpunktswinkel 90° erhalten.

Für welche Gewinnsituation würden Sie sich jetzt entscheiden?
6 P
Aufgabe W4b:
Ein quadratisches Blatt Papier (Format 10,0 cm x 10,0 cm) wird entlang von gefaltet. Die Strecke hat eine Länge von 4,0 cm.

Berechnen Sie die Länge nach der Faltung.
4 P