Home Geschichte Informatik Lernmaterial Linkliste Mathematik Smartphone ARS LB
2009 Übersicht
nach oben
Pflichtaufgaben
Aufgabe P1:
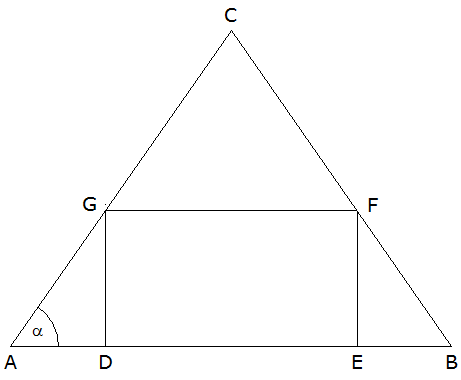
Gegeben ist ein gleichschenkliges Dreieck ABC mit einem einbeschriebenen Rechteck DEFG.

Es gilt:


Berechnen Sie den Flächeninhalt des Dreiecks GFC.
4,5 P
Aufgabe P2:
Die Dreiecke ABC und ABD haben die Seite gemeinsam.
Es gilt:
Berechnen Sie den Abstand des Punktes D von .
4 P
Aufgabe P3:
Ein zusammengesetzter Körper besteht aus einem Zylinder und einem Kegel.
Es gilt:
 

Berechnen Sie die Höhe des Zylinders.
4,5 P
Aufgabe P4:
Eine Gerade hat die Gleichung .  
    
Eine nach oben geöffnete Normalparabel hat den Scheitelpunkt .  
    
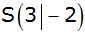Berechnen Sie die Koordinaten der Schnittpunkte von Gerade und Parabel.
Bestimmen Sie die Entfernung der Schnittpunkte rechnerisch.
4 P
Aufgabe P5:
Bestimmen Sie die Definitionsmenge und die Lösungsmenge der Gleichung:
 
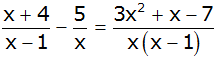3 P
Aufgabe P6:
Frau Schön legt einen Betrag von 10 000,00 € für die Dauer von vier Jahren zu einem Zinssatz von 4,2 % an. Zinsen werden mitverzinst.

Frau Reiche will ebenfalls 10 000,00 € anlegen. Die Zinsen sollen mitverzinst werden. Sie möchte jedoch schon nach drei Jahren das gleiche Endkapital wie Frau Schön angespart haben.

Welchen jährlich gleich bleibenden Zinssatz müsste Frau Reiche vereinbaren?
3 P
Aufgabe P7:
Die Jungen der Klasse 8a und 8b werden gemeinsam in einer Sportgruppe unterrichtet.

Beim Ballwurf werden von den 10 Schülern der 8a und den 13 Schülern der 8b folgende Weiten (Angaben in Meter) erzielt:
8a 41,5 27,5 32 39,5 32 29 27 42 51 22,5      
8b 33 19 26 36 25,5 41,5 36,5 30 39,5 29,5 29 45,5 25
Bestimmen Sie jeweils den Zentralwert und den Mittelwert (arithmetisches Mittel) der 8a und der 8b.

Paul aus der Klasse 8a, der am weitesten geworfen hat, wird aus der Wertung genommen, weil er einen zu leichten Ball verwendet hat.

Welche Auswirkungen hat dies auf den Zentralwert und das arithmetische Mittel der 8a?
3,5 P
Aufgabe P8:
In einem Gefäß befinden sich eine weiße, vier rote und fünf blaue Kugeln.
Es werden nacheinander zwei Kugeln ohne Zurücklegen gezogen.
Mit welcher Wahrscheinlichkeit werden zwei verschiedenfarbige Kugeln gezogen?
 
Wie groß ist die Wahrscheinlichkeit, dass höchstens eine der gezogenen Kugeln rot ist?
3,5 P
Wahlaufgaben
Aufgabe W1a:
Auf einem Würfel liegt der Streckenzug RSTU mit der Länge 21,7 cm.
Es gilt:
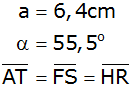Berechnen Sie die Länge von .
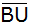6 P
Aufgabe W1b:
Gegeben ist das rechtwinklige Dreieck ABC.
Es gilt:
Zeigen Sie ohne Verwendung gerundeter Werte, dass der Umfang des Dreiecks ABC mit der Formel

berechnet werden kann.
4 P
Aufgabe W2a:
Von einer regelmäßigen fünfseitigen Pyramide sind gegeben:
Berechnen Sie den Flächeninhalt des Dreiecks AFS.
5,5 P
Aufgabe W2b:
Ein zusammengesetzter Körper besteht aus einer Halbkugel und aus einem Kegel.
Berechnen Sie die Oberfläche des zusammengesetzten Körpers.
4,5 P
Aufgabe W3a: 
Eine nach oben geöffnete Normalparabel 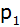verläuft durch die Punkte 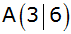und .
 
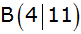Diese Parabel wird um 5 Einheiten nach links und um 5 Einheiten nach unten verschoben.
Dadurch entsteht die Parabel 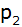mit dem Scheitelpunkt .
 
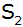Die beiden Parabeln haben einen gemeinsamen Punkt .
 
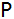Berechnen Sie die Entfernung der Punkte 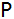und .
 
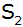5,5 P 
Aufgabe W3b:
Der Scheitelpunkt einer nach oben geöffneten Normalparabel hat die Koordinaten .
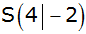Der Punkt 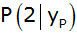liegt auf der Parabel. Er bildet mit den Punkten 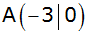und ein Dreieck.
 
Berechnen Sie den Flächeninhalt des Dreiecks ABP.
 
Der Punkt 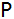wird auf der Parabel verschoben.
Es gibt zwei Dreiecke 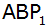und 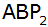, deren Flächeninhalt jeweils 20,5 FE (Flächeneinheiten) beträgt.
 
Berechnen Sie die Koordinaten der beiden Punkte 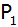und .
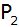4,5 P
Aufgabe W4a:
                                        
Zwei Spielwürfel werden geworfen.
Die beiden gewürfelten Augenzahlen werden addiert (Augensummen).
 
Welche Wahrscheinlichkeit hat das Ereignis "Augensumme kleiner als 5"?
 
Bei einem Pasch sind die Augenzahlen gleich.
Wie groß ist die Wahrscheinlichkeit keinen Pasch zu werfen?
 
Nennen Sie zwei Ereignisse, für die sich die Wahrscheinlichkeit 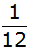ergibt.
6 P
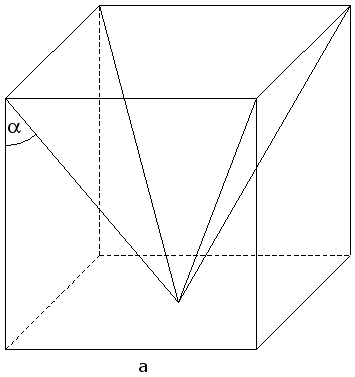
Aufgabe W4b:
Aus einem Würfel wurde eine quadratische Pyramide herausgearbeitet.
Es gilt:
Zeigen Sie, dass die Oberfläche des Restkörpers mit der Formel

                                        

berechnet werden kann.

 
Weisen Sie nach, dass gilt:

                                         

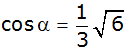
4 P