|
Pflichtaufgaben |
|
Aufgabe P1: |
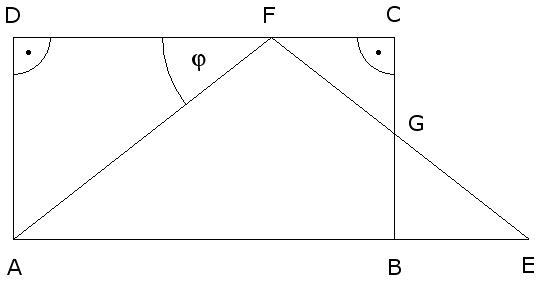
| Gegeben sind
das Rechteck ABCD und das gleichschenklige Dreieck
AEF. |
|
Es gilt: |
|
 |
|
| Berechnen Sie
den Flächeninhalt des Dreiecks BEG. |
|
|
 |
4,5 P |
|
|
Aufgabe P2: |
| Vom Viereck
ABCD sind bekannt: |
|
|
Berechnen Sie den
Abstand des Punktes D von
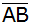 . . |
Berechnen
Sie die Länge
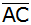 . . |
|
|
 |
4 P |
|
|
Aufgabe P3: |
| Von einer
regelmäßigen fünfseitigen Pyramide sind bekannt: |
|
|
| Berechnen Sie
das Volumen der Pyramide. |
|
|
 |
4 P |
|
|
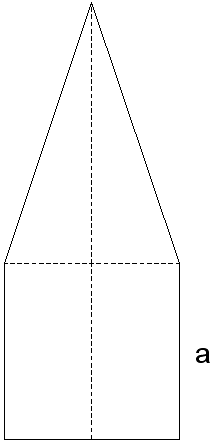
Aufgabe P4: |
| Ein
zusammengesetzter Körper besteht aus einem Zylinder
und einem Kegel. |
| Der
Achsenschnitt des Zylinders ist ein Quadrat. |
| Es gilt: |
|
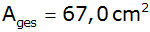 |
(Flächeninhalt
der nebenstehenden Achsenschnittfläche) |
|
 |
|
|
| Berechnen Sie
die Oberfläche des zusammengesetzten Körpers. |
|
|
 |
4 P |
|
|
Aufgabe P5: |
| Geben Sie die
Definitionsmenge und die Lösungsmenge der Gleichung
an: |
| |
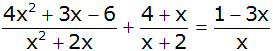 |
|
|
3,5
P |
|
|
|
|
Aufgabe P7: |
Gabi legt bei ihrer Bank 2500,00 € zu folgenden Zinssätzen
auf drei Jahre an:
| |
1. Jahr: |
3,50 % |
| |
2. Jahr: |
3,75 % |
| |
3. Jahr |
4,25 % |
| |
Zinsen werden mitverzinst. |
Das angesparte Geld lässt sie nach Ablauf der drei Jahre
ein weiteres Jahr bei der Bank.
Für dieses vierte Jahr
erhält sie 132,93 € Zinsen.
Wie hoch ist der Zinssatz im vierten Jahr?
|
|
3 P |
|
|
Aufgabe P8: |
|
In einem Behälter liegen fünf blaue, drei weiße und zwei
rote Kugeln. Mona zieht eine Kugel, notiert die Farbe und
legt die Kugel wieder zurück.
Danach zieht sie eine
zweite Kugel.
|
• |
Wie groß ist
die Wahrscheinlichkeit, dass zwei gleichfarbige
Kugeln gezogen werden? |
| |
|
|
• |
Wie groß ist
die Wahrscheinlichkeit, dass von den beiden
gezogenen Kugeln eine rot und eine weiß ist? |
|
|
4 P |
|
|
Wahlaufgaben |
|
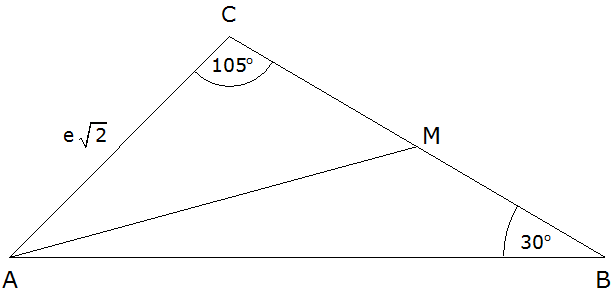
Aufgabe W1a: |
| Gegeben ist
das Trapez ABCD. |
|
Es gilt: |
| |
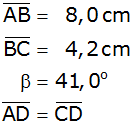 |
|
Berechnen Sie
den Winkel  . . |
|
|
 |
5,5
P |
|
|
|
 |
4,5
P |
|
|
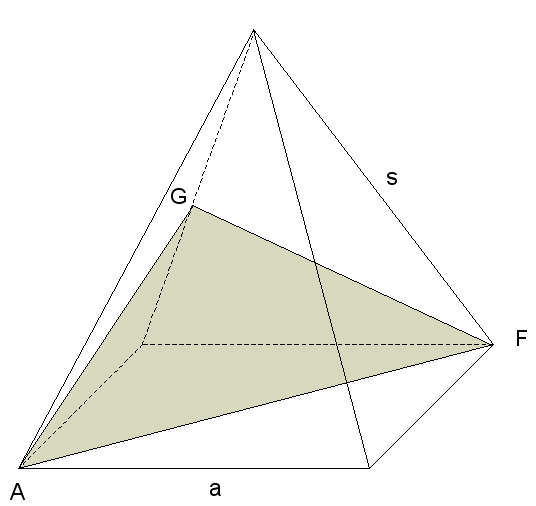
Aufgabe W2a: |
| Von einer
quadratischen Pyramide sind bekannt: |
|
|
| Der Punkt G
halbiert die Seitenkante s. |
| |
| Berechnen Sie
den Umfang des Dreiecks AFG. |
|
|
 |
5,5
P |
|
|
Aufgabe W2b: |
|
Aus einem massiven Kegel wurde ein Teil
ausgeschnitten. |
| Es
gilt: |
|
|
| |
|
Zeigen Sie ohne Verwendung gerundeter Werte, dass
die Oberfläche des neu entstandenen Körpers um |
| |
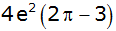 |
|
kleiner ist. |
|
|
 |
4,5
P |
|
|
Aufgabe W3a: |
Eine Parabel  hat
die Gleichung hat
die Gleichung  . . |
Eine nach oben
geöffnete Normalparabel  hat
den Scheitel hat
den Scheitel  . . |
| |
| Durch die
gemeinsamen Punkte der beiden Parabeln verläuft eine
Gerade. |
| |
| |
| Bestimmen Sie
die Gleichung dieser Geraden rechnerisch. |
| |
| Berechnen Sie
die Winkel, unter denen die Gerade die x-Achse
schneidet. |
|
|
5,5 P |
|
|
Aufgabe W3b: |
Von einer nach oben geöffneten Normalparabel  sind
die Schnittpunkte mit der x-Achse bekannt: sind
die Schnittpunkte mit der x-Achse bekannt: |
| |
 und und 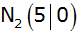 |
| |
Durch den Scheitelpunkt der Parabel  verläuft
die Gerade verläuft
die Gerade  mit
der Steigung mit
der Steigung  . . |
| |
|
Auf dieser Geraden liegt der Scheitelpunkt einer
zweiten nach oben geöffneten Normalparabel, die mit
der x-Achse nur einen gemeinsamen Punkt hat. |
| |
|
Berechnen Sie die Koordinaten des Schnittpunkts der
beiden Parabeln. |
|
|
4,5
P |
|
|
Aufgabe W4a: |
| Ein Glücksrad
mit den Mittelpunktswinkeln 60°; 120° und 180° ist
mit den Zahlen 20; 10 und 6 beschriftet. |
| Es wird
zweimal gedreht. |
| |
| Wie groß ist
die Wahrscheinlichkeit, dass die Summe der
erhaltenen Zahlen genau 30 ergibt? |
| |
| Wie groß ist
die Wahrscheinlichkeit, dass die Summe größer als 12
ist? |
| |
| Mit welcher
Wahrscheinlichkeit ist die Summe kleiner als 30? |
|
|
 |
6 P |
|
|
Aufgabe W4b: |
Das regelmäßige Sechseck hat die Seitenlänge 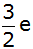 . . |
| |
|
Die vier grau eingefärbten Dreiecke bilden die
Mantelfläche einer quadratischen Pyramide. |
| |
|
Berechnen Sie ohne Verwendung gerundeter Werte das
Volumen der Pyramide in Abhängigkeit von e. |
| |
Der Neigungswinkel zwischen einer Seitenfläche und
der Grundfläche der Pyramide wird mit 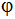 bezeichnet. bezeichnet. |
| |
|
Zeigen Sie, dass gilt: |
| |
| |
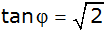 |
|
|
 |
4 P |
|