|
Pflichtaufgaben |
|
Aufgabe P1: |
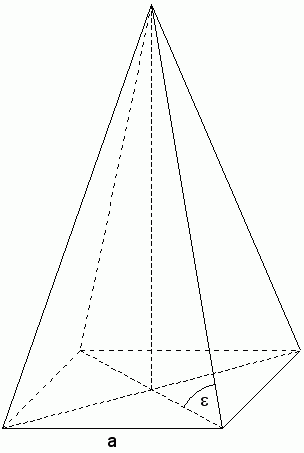
| Von einer
quadratischen Pyramide sind gegeben: |
|
|
Berechnen Sie
den Winkel 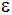 zwischen
der Seitenkante und der Grundfläche der Pyramide. zwischen
der Seitenkante und der Grundfläche der Pyramide. |
|
|
 |
2 P |
|
|
Aufgabe P2: |
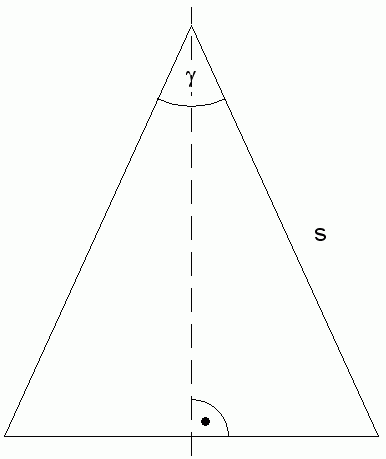
| Die Skizze
zeigt den Achsenschnitt eines Kegels. |
| Es gilt: |
|
|
| Eine Kugel hat
das gleiche Volumen wie der Kegel. |
| Berechnen Sie
den Radius der Kugel. |
|
|
 |
2 P |
|
|
Aufgabe P3: |
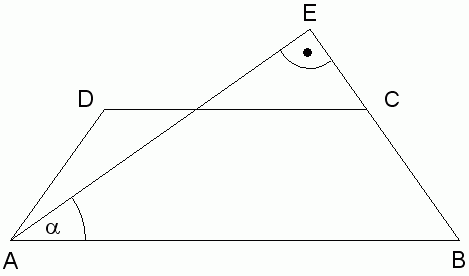
| Gegeben sind
das gleichschenklige Trapez ABCD und das
rechtwinklige Dreieck ABE. |
| Es gilt: |
|
|
Berechnen Sie
die Länge 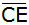 . . |
|
|
 |
2,5
P |
|
|
Aufgabe P4: |
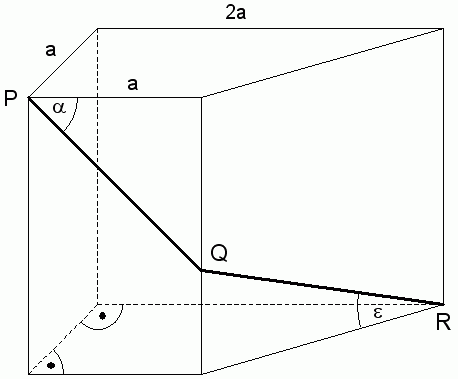
| Auf dem Prisma
liegt der Streckenzug PQR mit der Länge 9,1 cm. |
| Es gilt: |
|
|
Berechnen Sie
den Winkel 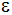 . . |
|
|
 |
2 P |
|
|
|
|
Aufgabe P6: |
Eine Parabel
hat die Gleichung 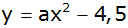 und
geht durch den Punkt und
geht durch den Punkt  . . |
| Berechnen Sie a. |
| Zeichnen Sie
das Schaubild der Parabel in ein Koordinatensystem. |
| Berechnen Sie
die Koordinaten der Schnittpunkte von Parabel und
x-Achse |
|
|
2,5
P |
|
|
Aufgabe P7: |
Der Mehrwertsteuersatz wurde in Deutschland am 1.1.2007 von
16% auf 19% angehoben.
Der Endpreis eines Mountainbikes hat sich dadurch um 40,50 €
erhöht.
Wie viel Euro kostet jetzt das Mountainbike einschließlich
der Mehrwertsteuer?
Guido behauptet: Der Endpreis hat sich durch die Erhöhung
der Mehrwertsteuer um 3% erhöht.
Überprüfen Sie diese
Behauptung.
|
|
2 P |
|
|
Aufgabe P8: |
Ein Guthaben von 5 000,00 € wird für drei Jahre angelegt.
Zinsen werden mitverzinst.Die Zinssätze der ersten beiden
Jahre sind:
| |
Zinssatz im 1.
Jahr: |
2,5% |
| |
Zinssatz im 2.
Jahr: |
3,25% |
Für die drei Jahre werden insgesamt 503,23 € Zinsen
gutgeschrieben.
Wie hoch ist der Zinssatz im dritten Jahr?
Bei welchem jährlich gleichbleibenden Zinssatz wäre nach
drei Jahren das gleiche Endkapital erzielt worden?
|
|
2 P |
|
|
Wahlaufgaben |
|
Aufgabe W1a: |
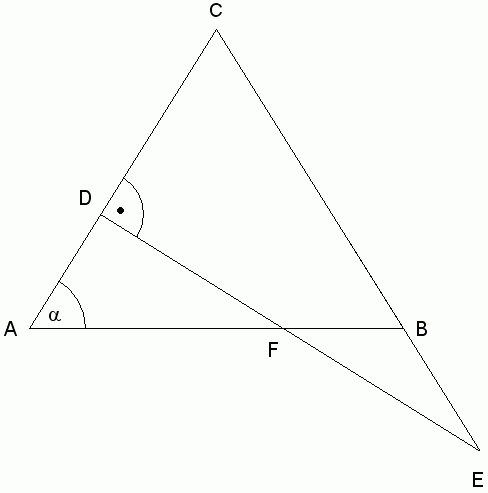
| Gegeben sind
das gleichschenklige Dreieck ABC und das
rechtwinklige Dreieck CDE. Es gilt:
|
|
|
| Berechnen Sie
den Flächeninhalt des Dreiecks BFE. |
|
|
 |
5 P |
|
|
Aufgabe W1b: |
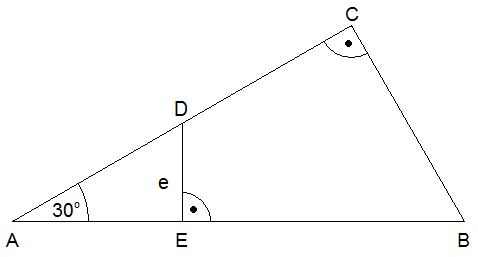
Im
rechtwinkligen Dreieck ABC ist D der Mittelpunkt der
Seite 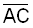 . .
Zeigen Sie ohne Verwendung gerundeter Werte, dass
der Flächeninhalt des Vierecks EBCD mit der Formel
|
|
|
| berechnet
werden kann. |
|
|
 |
3 P |
|
|
|
|
Aufgabe W2b: |
|
Geben Sie die Definitionsmenge
und die Lösungsmenge der Gleichung an: |
|
|
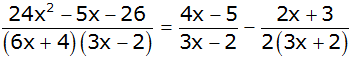
|
|
|
3 P |
|
|
Aufgabe W3a: |
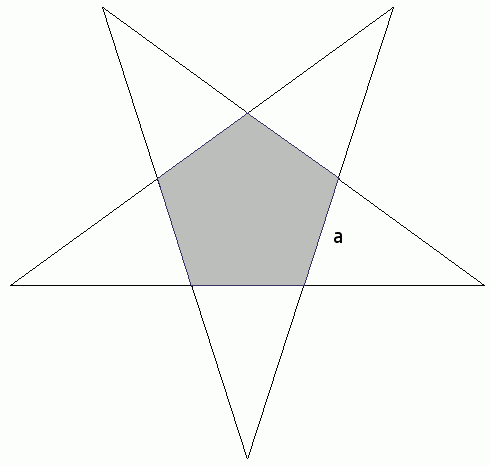
| Ein
regelmäßiges Fünfeck hat die Seitenlänge a = 3,6 cm.
Verlängert man alle Fünfeckseiten, so entsteht das
Netz einer regelmäßigen Pyramide.
Berechnen Sie die
Mantelfläche und das Volumen der Pyramide.
|
|
|
 |
5 P |
|
|
Aufgabe W3b: |
|
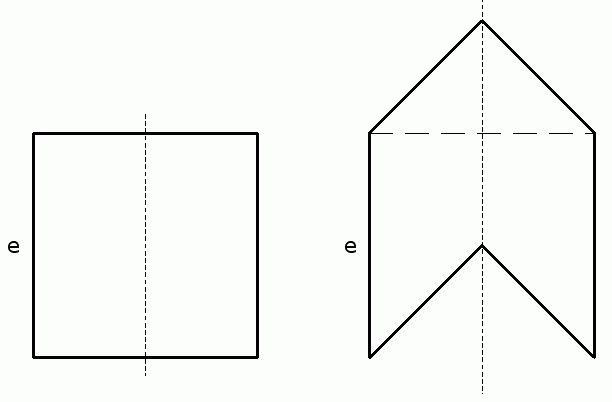
Der Achsenschnitt eines Zylinders ist
ein Quadrat mit der Seitenlänge e.
Aus dem Zylinder wird ein Kegel mit
halber Zylinderhöhe herausgearbeitet und oben aufgesetzt.
Weisen Sie nach, dass die Oberfläche
des neu entstandenen Körpers um

größer ist als die des Zylinders.
|
|
 |
3 P |
|
|
|
|
Aufgabe W4b: |
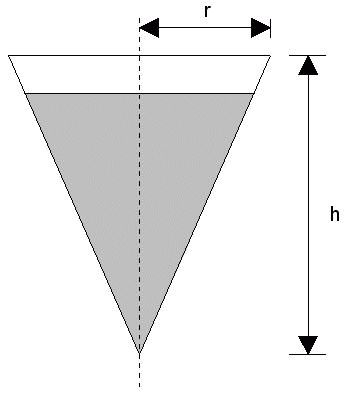
| Ein
kegelförmiges Gefäß ist gegeben durch: |
|
|
Es ist zu 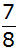 seiner
Höhe mit Wasser gefüllt. seiner
Höhe mit Wasser gefüllt. |
| Eine Kugel
taucht vollständig in das Gefäß ein. Dadurch steigt
der Wasserspiegel genau bis zum Rand des Gefäßes. |
| Bestimmen Sie
den Radius der Kugel. |
|
|
 |
4 P |
|