Home Geschichte Informatik Lernmaterial Linkliste Mathematik Smartphone ARS LB
2005 Übersicht
nach oben
Pflichtaufgaben
Aufgabe P1:
Von einer quadratischen Pyramide sind bekannt:
 
Berechnen Sie das Volumen der Pyramide.
1,5 P
Aufgabe P2:
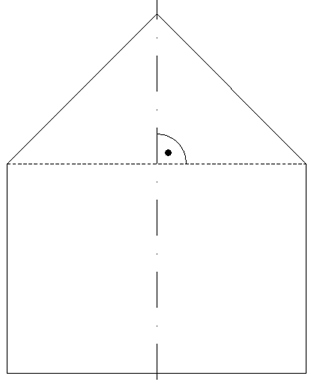
Ein zusammengesetzter Körper besteht aus einem Zylinder mit aufgesetztem Kegel.
Für den Kegel gilt:
 
 
Die Höhe des Zylinders ist gleich lang wie die Mantellinie des Kegels.
 
Berechnen Sie die Oberfläche des zusammengesetzten Körpers.
2,5 P
Aufgabe P3:
Lösen Sie die Gleichung:

 
2 P
Aufgabe P4:
Eine Gerade  hat die Gleichung .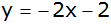
Eine zweite Gerade 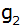 hat die Steigung 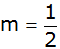 und schneidet die y-Achse im Punkt .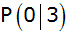
 
Der Schnittpunkt der beiden Geraden ist Scheitelpunkt einer nach oben geöffneten Normalparabel .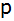
 
Berechnen Sie die Gleichung der Parabel.
2 P
Aufgabe P5:
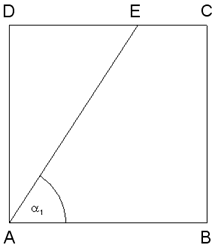
Das Viereck ABCD ist ein Quadrat.
 
Es gilt:
 
 
Berechnen Sie die Länge  .
2 P
Aufgabe P6:
Auf der Geraden AD liegen die Dreiecke ABC und BDE.
 
Es gilt:
   
 
 
Berechnen Sie die Länge .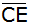
2,5 P
Aufgabe P7:
Ulrike legt bei ihrer Bank einen Betrag von 8 000,00 € für drei Jahre an.
Zinsen werden mitverzinst.
 
Bis zum Ende der drei Jahre wächst ihr Guthaben um insgesamt 8,73% an.
 
Im ersten Jahr beträgt der Zinssatz 2,0%. Im zweiten Jahr werden 204,00 € Zinsen gutgeschrieben.
 
Wie hoch ist der Zinssatz im dritten Jahr?
2 P
Aufgabe P8:
Die Mietpreise für Wohnungen in einer Großstadt und in einer Kleinstadt werden verglichen. Bei den aufgeführten Wohnungen sind die Mieten in der Kleinstadt stets um den gleichen Prozentsatz niedriger als in der Großstadt.
 

 
Um wie viel Prozent ist die Miete für die 4-Zimmer-Wohnung in der Kleinstadt niedriger als in der Großstadt?
 
Wie hoch ist die Miete der 2-Zimmer-Wohnung in der Großstadt?
 
Die Miete der 1-Zimmer-Wohnung ist in der Kleinstadt um 54 € niedriger als in der Großstadt. Berechnen Sie beide Mietpreise.
2,5 P
Wahlaufgaben
Aufgabe W1a:
Für die quadratische Pyramide gilt:
 
 
 
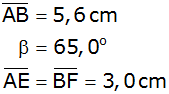Berechnen Sie die Länge 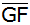 sowie den Flächeninhalt des Vierecks BCGF.
5 P
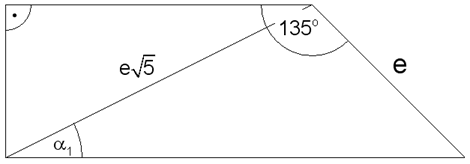
Aufgabe W1b:
Gegeben ist ein rechtwinkliges Trapez.
 
Zeigen Sie ohne Verwendung gerundeter Werte, dass gilt:
 
3 P
Aufgabe W2a:
Eine Parabel 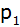 hat die Gleichung .
Durch den Scheitelpunkt der Parabel und durch den Punkt 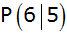 geht die Gerade .
 
Berechnen Sie die Gleichung der Geraden .
 
Eine zweite nach oben geöffnete Normalparabel  hat den Scheitelpunkt .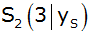
Er liegt auf der Geraden .
 
Berechnen Sie die Koordinaten des Schnittpunktes 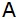 beider Parabeln.
 
 
Durch den Schnittpunkt 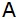 verläuft eine zu  parallele Gerade .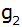
Die Gerade 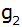 schneidet die Parabel   in einem weiteren Punkt.
 
Berechnen Sie dessen Koordinaten.
5 P
Aufgabe W2b:
Bestimmen Sie die Definitionsmenge und die Lösungsmenge der Gleichung:  

     

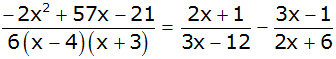
3 P
Aufgabe W3a:

Von einer regelmäßigen neunseitigen Pyramide sind bekannt:
 
Berechnen Sie das Volumen der Pyramide.
4 P
Aufgabe W3b:
Ein Kreis wird in zwei Kreisausschnitte geteilt. Die Ausschnitte bilden jeweils den Mantel eines Kegels (siehe Skizze).
   
Für Kegel 1 gilt:
 
Zeigen Sie ohne Verwendung gerundeter Werte, dass für den Radius von Kegel 2 gilt:
 
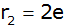4 P
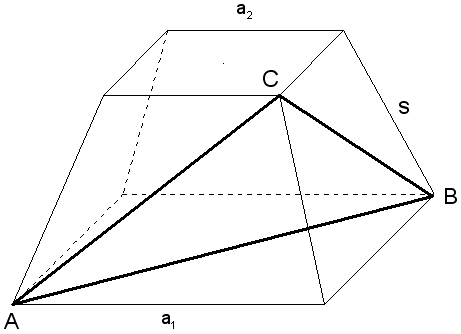
Aufgabe W4a:

Von einem quadratischen Pyramidenstumpf sind bekannt:
 
Berechnen Sie den Flächeninhalt des Dreiecks ABC.
4 P
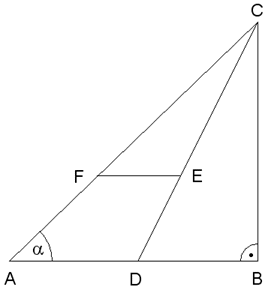
Aufgabe W4b:

Im Dreieck ABC liegt das Trapez ADEF.
Gegeben sind:
 
Berechnen Sie den Flächeninhalt des Trapezes ADEF.
4 P