|
Pflichtaufgaben |
|
Aufgabe P1: |
| Im Viereck
ABCD sind gegeben: |
|
|
| |
| |
| |
Berechnen Sie
den Winkel  . . |
| Wie groß ist
der Flächeninhalt des Dreiecks ACD? |
|
|
 |
2 P |
|
|
Aufgabe P2: |
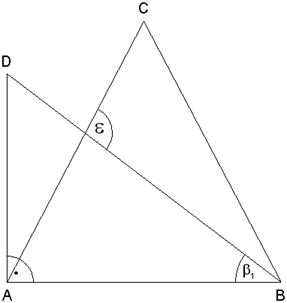
Das
rechtwinklige Dreieck ABD und das gleichschenklige
Dreieck ABC haben die Seite 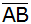 gemeinsam. gemeinsam. |
| Es gilt: |
|
|
| |
Berechnen Sie
den Winkel 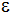 . . |
|
|
 |
2,5
P |
|
|
|
|
Aufgabe P4: |
Eine Parabel
hat die Funktionsgleichung 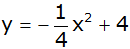 . . |
| Zeichnen Sie
das Schaubild der Parabel in ein Koordinatensystem. |
| |
| Die drei
Schnittpunkte der Parabel mit den Koordinatenachsen
bilden ein Dreieck. |
| Berechnen Sie
den Umfang des Dreiecks. |
|
|
2 P |
|
|
Aufgabe P5: |
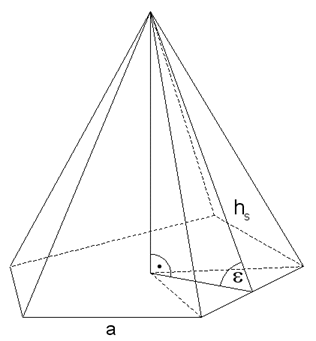
Von einer regelmäßigen fünfseitigen
Pyramide sind gegeben:
Berechnen Sie die Höhe 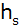 der
Seitenfläche und den Winkel der
Seitenfläche und den Winkel 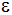 . . |
|
 |
2 P |
|
|
Aufgabe P6: |
| Eine Kugel und
ein Zylinder werden miteinander verglichen: |
|
| |
- die
Kugel hat das Volumen 268 cm3, |
| |
- der
Radius der Kugel und der Grundkreisradius
des Zylinders sind gleich lang, |
| |
- die
Oberfläche der Kugel und die Mantelfläche
des Zylinders sind gleich groß. |
|
|
| Berechnen Sie
die Differenz der beiden Rauminhalte. |
|
|
2,5
P |
|
|
Aufgabe P7: |
|
Corinna legt 4 500,00 € zu folgenden Zinssätzen auf drei
Jahre an: |
| |
1. Jahr 1,50%
2. Jahr
2,25%
3. Jahr 2,75%
Zinsen werden mitverzinst. |
|
|
Hans legt ebenfalls 4 500,00 € auf drei Jahre an. Nach
Ablauf des ersten Jahres erhält er 45,00 € Zinsen, nach
Ablauf des zweiten Jahres 91,43 €. |
|
Zinsen werden mitverzinst. |
|
Welchen Zinssatz muss seine Bank im dritten Jahr gewähren,
damit er nach den drei Jahren das gleiche Guthaben wie
Corinna hat? |
|
2 P |
|
|
Aufgabe P8: |
| Eine Schule
nutzt das nebenstehende Angebot und kauft fünf
Druckerpatronen. |
| Vom Preis
einschließlich 16% Mehrwertsteuer dürfen 2% Skonto
abgezogen werden. |
| Es sind dann
205,20 € zu überweisen. |
| Wie hoch ist
der Katalogpreis für eine Einzelpatrone ohne den
Mengenrabatt? |
|
|
 |
2 P |
|
|
Wahlaufgaben |
|
Aufgabe W1a: |
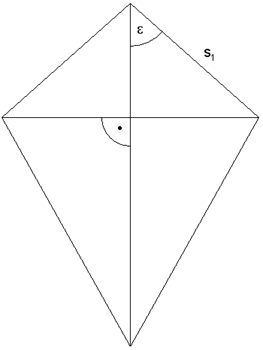
| Ein Körper
besteht aus zwei quadratischen Pyramiden mit
gemeinsamer Grundfläche. |
| Die Skizze
zeigt den Diagonalschnitt des Körpers. |
|
Gegeben sind: |
| |
 |
| |
Das
Volumen der unteren Pyramide ist doppelt so
groß wie das der oberen. |
|
| Berechnen Sie
die Oberfläche des Körpers. |
|
|
 |
5 P |
|
|
Aufgabe W1b: |
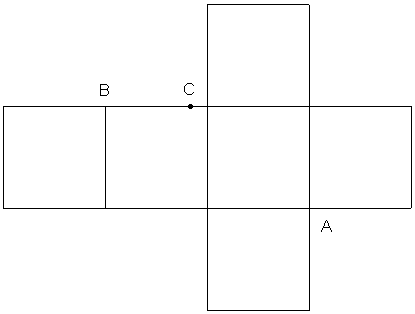
| Die Zeichnung
stellt das Netz eines Würfels mit der Kanten-länge a
dar. |
| Es gilt: |
|
|
| Zeichnen Sie
ein Schrägbild des Körpers mit dem Dreieck ABC
maßgerecht für a = 6 cm. |
| Zeigen Sie,
dass sich der Flächeninhalt dieses Dreiecks in
Abhängigkeit von a mit der Formel berechnen lässt: |
|
|
Berechnen Sie
die Länge der Strecke 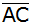 im
Körper in Abhängigkeit von a ohne Verwendung
gerundeter Werte. im
Körper in Abhängigkeit von a ohne Verwendung
gerundeter Werte. |
|
|
 |
3 P |
|
|
Aufgabe W2a: |
Die Parabel 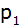 hat
die Funktionsgleichung hat
die Funktionsgleichung 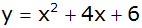 . . |
Verschiebt man
diese Parabel um drei Einheiten nach rechts und um
drei Einheiten nach unten, entsteht die Parabel 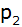 mit
dem Scheitelpunkt mit
dem Scheitelpunkt 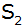 . . |
Berechnen Sie
die Koordinaten des Schnittpunkts 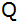 der
beiden Parabeln. der
beiden Parabeln. |
Durch 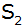 und und 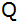 verläuft
die Gerade verläuft
die Gerade 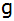 . . |
Die Gerade 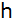 verläuft
parallel zur Geraden verläuft
parallel zur Geraden 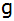 und
geht durch den Scheitelpunkt und
geht durch den Scheitelpunkt 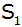 der
Parabel der
Parabel 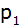 . . |
Bestimmen Sie
rechnerisch die Gleichung der Geraden 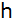 . . |
|
|
5 P |
|
|
Aufgabe W2b: |
| Bestimmen Sie
die Definitionsmenge und die Lösungsmenge der
Gleichung: |
|
|
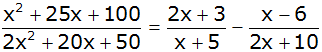
|
|
|
3 P |
|
|
Aufgabe W3a: |
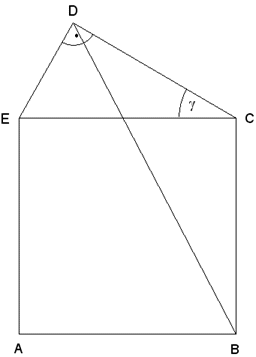
| Das Fünfeck
ABCDE besteht aus einem Quadrat und einem
rechtwinkligen Dreieck. |
| Gegeben sind: |
|
|
Berechnen Sie
die Länge 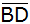 und
den Flächeninhalt des Vierecks ABDE. und
den Flächeninhalt des Vierecks ABDE. |
|
|
 |
4,5
P |
|
|
Aufgabe W3b: |
| Im Rechteck
ABCD gilt: |
|
|
| Zeigen Sie,
dass sich der Flächeninhalt des Vierecks ASED mit
der Formel berechnen lässt: |
|
|
|
|
 |
3,5
P |
|
|
Aufgabe W4a: |
|
Das Bild zeigt Parabeln und Geraden. |
|
Ordnen Sie jedem Schaubild die richtige
Funktionsgleichung zu. |
|
Begründen Sie ihre Entscheidungen. |
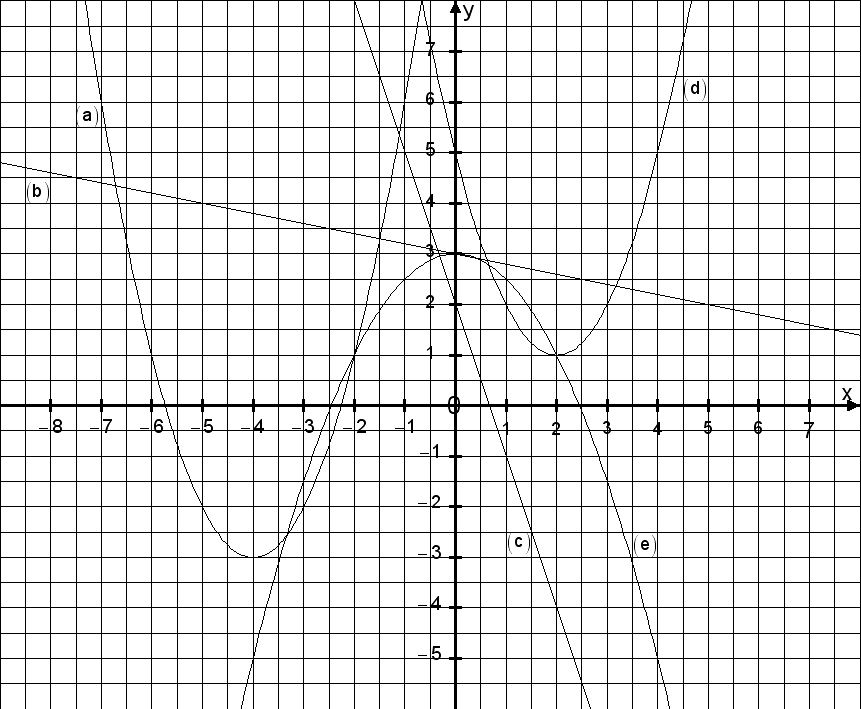 |
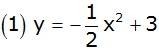 |
 |
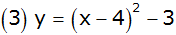 |
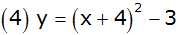 |
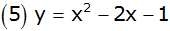 |
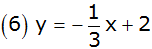 |
 |
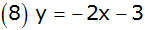 |
 |
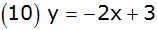 |
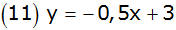 |
 |
|
| |
|
4 P |
|
|
Aufgabe W4b: |
| Ein massiver
Körper hat die Form eines Kegelstumpfs. |
| Aus ihm wird
ein Teilkörper herausgearbeitet (siehe Skizze). |
| Die Maße des
Kegelstumpfes sind: |
|
|
| Um wie viel
Prozent hat sich die Oberfläche verändert? |
|
|
 |
4 P |
|