|
Pflichtaufgaben |
|
Aufgabe P1: |
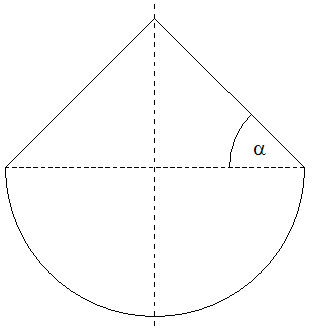
Ein Körper
besteht aus einer Halbkugel und einem aufgesetzten
Kegel mit 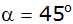 (siehe
Achsenschnitt). (siehe
Achsenschnitt).
Das Volumen der Halbkugel beträgt 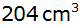 . . |
| Berechnen Sie
die Oberfläche des Körpers. |
|
|
 |
2
P |
|
|
Aufgabe P2: |
| Ein
quadratisches Prisma und eine quadratische Pyramide
haben gleich große Grundflächen. |
| |
Das Prisma hat
die Höhe h = 5,0 cm und die Grundkante a = 3,0 cm.
Das Volumen der Pyramide ist halb so groß wie das
Volumen des Prismas. |
| |
| Berechnen Sie
die Höhe der Pyramide. |
|
|
2 P |
|
|
Aufgabe P3: |
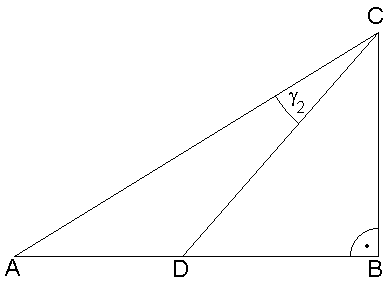
| Im
rechtwinkligen Dreieck ABC sind gegeben: |
| |
|
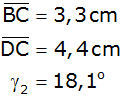
|
| |
| Berechnen Sie
den Flächeninhalt des Dreiecks ADC. |
|
|
 |
2 P |
|
|
|
|
Aufgabe P5: |
| Bestimmen Sie
die Definitions- und die Lösungsmenge der Gleichung: |
| |
|
|
|
|
2 P |
|
|
Aufgabe P6: |
Eine nach oben
geöffnete Normalparabel hat den Scheitelpunkt 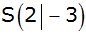 . . |
Die Gerade g
hat die Steigung m = 1 und schneidet die Parabel in 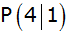 . . |
| |
| Berechnen Sie
die Koordinaten des zweiten Schnittpunkts von
Parabel und Gerade. |
|
|
2,5
P |
|
|
Aufgabe P7: |
| Karl-Anton
legt am Anfang eines Jahres einen bestimmten
Geldbetrag bei der Bank an. |
| Der jährlich
gleich bleibende Zinssatz beträgt 3,5%. Zinsen
werden mitverzinst. |
| |
| Nach Ablauf
des ersten Jahres hebt er 700,00 € ab, nach Ablauf
des zweiten Jahres 500,00 €. |
| |
| Am Ende des
dritten Jahres beträgt sein Sparguthaben 3 721,87 €. |
| |
| Berechnen Sie
den ursprünglich angelegten Betrag. |
|
|
2 P |
|
|
Aufgabe P8: |
|
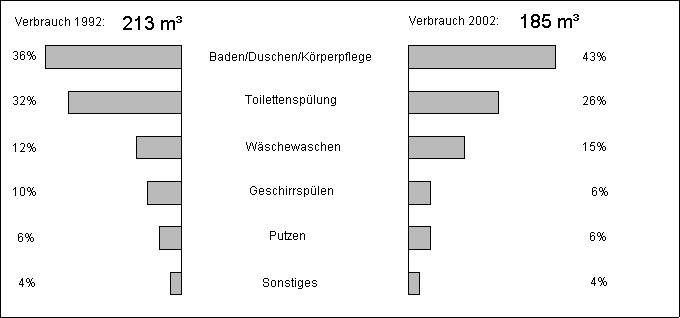
Das Diagramm zeigt die Aufteilung des
Wasserverbrauchs eines Vier-Personen-Haushalts in
den Jahren 1992 und 2002. |
 |
|
Um wieviel Prozent liegt der Wasserverbrauch 2002
unter dem von 1992? |
|
Wie viel m³ Wasser wurden im Jahr 2002 für die
Toilettenspülung weniger verbraucht als 1992? |
|
Wie viel Liter Wasser wurden in dem Haushalt im Jahr
2002 für das Geschirrspülen pro Tag durchschnittlich
verbraucht? |
|
|
2 P |
|
|
Wahlaufgaben |
|
Aufgabe W1a: |
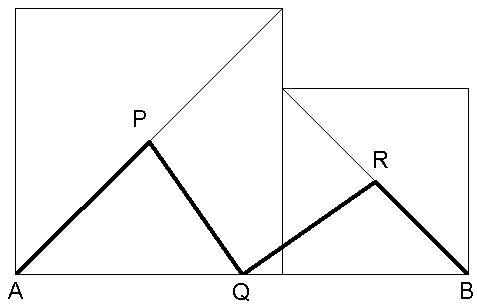
| Zwei Quadrate
mit den Seitenlängen 10,0 cm bzw. 7,0 cm werden wie
rechts skizziert aneinandergelegt. |
| |
P und R sind
die Mittelpunkte der Diagonalen, Q ist der
Mittelpunkt der Strecke 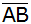 . . |
| |
| Berechnen Sie
die Länge des Streckenzuges APQRB und die Größe des
Winkels RQP. |
|
|
 |
4,5 P |
|
|
Aufgabe W1b: |
Die Punkte 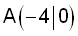 und und 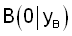 bilden
mit dem Koordinatenursprung ein rechtwinkliges
Dreieck. Der Punkt B ist auf der y-Achse beweglich. bilden
mit dem Koordinatenursprung ein rechtwinkliges
Dreieck. Der Punkt B ist auf der y-Achse beweglich.
Der Innenwinkel des Dreiecks bei A wird mit 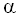 bezeichnet. bezeichnet. |
| |
Der Winkel 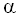 ist
von ist
von 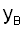 abhängig.
Tabellieren Sie diese Abhängigkeit des Winkels abhängig.
Tabellieren Sie diese Abhängigkeit des Winkels 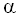 für für 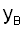 von
0 bis 7 in Einerschritten. von
0 bis 7 in Einerschritten.
Zeichnen Sie das
zugehörige Schaubild. |
| |
Wie groß ist
jeweils 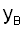 ,
wenn ,
wenn 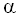 die
Werte 30° bzw. 60° annimmt? die
Werte 30° bzw. 60° annimmt? |
| |
Welchen
Flächeninhalt hat das Dreieck jeweils, wenn 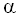 die
Werte 30° bzw. 60° annimmt? die
Werte 30° bzw. 60° annimmt? |
|
|
3,5
P |
|
|
Aufgabe W2a: |
| Gegeben ist
ein Kegelstumpf mit: |
| |
|
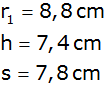
|
| |
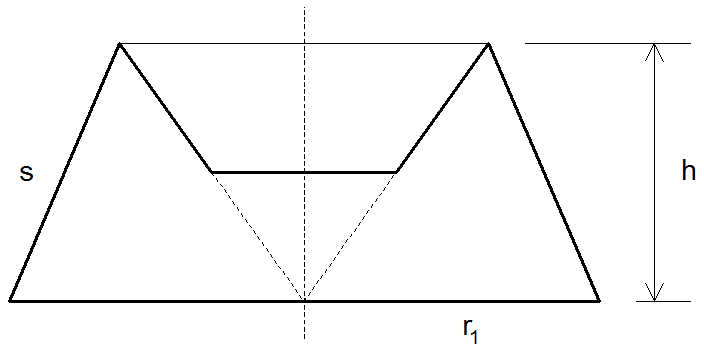
| Aus diesem
Kegelstumpf wird bis zur halben Höhe ein weiterer
Kegelstumpf herausgearbeitet (siehe Skizze). |
| |
| Um wie viel
cm² vergrößert sich dadurch die Oberfläche des
Körpers? |
|
|
 |
4,5
P |
|
|
Aufgabe W2b: |
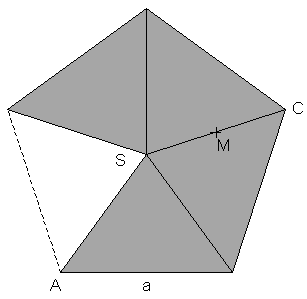
| Die vier
dunkel eingefärbten Teilflächen eines regelmäßigen
Fünfecks mit der Seitenlänge a = 7,6 cm bilden den
Mantel einer quadratischen Pyramide. |
| |
| Berechnen Sie
das Volumen der Pyramide. |
| |
Der Punkt M
liegt auf der Mitte von  . . |
| |
Berechnen Sie
die Länge von 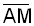 im
Körper. im
Körper. |
|
|
 |
3,5
P |
|
|
Aufgabe W3a: |
Die
Normalparabel 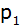 hat
die Gleichung hat
die Gleichung 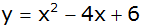 . . |
Die
Normalparabel 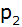 ist
nach unten geöffnet und hat den Scheitel ist
nach unten geöffnet und hat den Scheitel 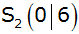 . . |
| |
Durch die
Schnittpunkte beider Parabeln verläuft die Gerade 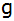 . . |
| Bestimmen Sie
rechnerisch die Gleichung der Geraden. |
| |
| Die Gerade
bildet mit den Koordinatenachsen ein rechtwinkliges
Dreieck. |
| Berechnen Sie
die restlichen Innenwinkel und den Umfang des
Dreiecks. |
|
|
4,5
P |
|
|
Aufgabe W3b: |
| Bestimmen Sie
die Definitionsmenge und die Lösungsmenge der
Gleichung: |
|
|
|
|
3,5
P |
|
|
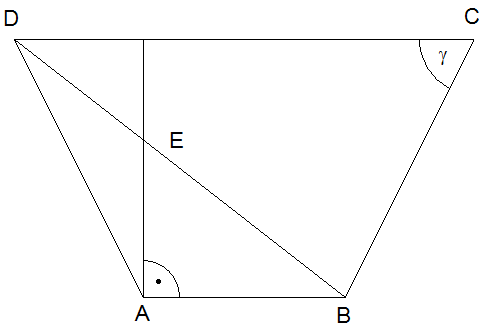
Aufgabe W4a: |
| Vom
gleichschenkligen Trapez ABCD sind gegeben: |
| |
|
|
| |
Berechnen Sie
die Länge 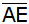 . . |
| |
Welchen
Abstand hat E von 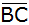 ? ? |
|
|
 |
4,5
P |
|
|
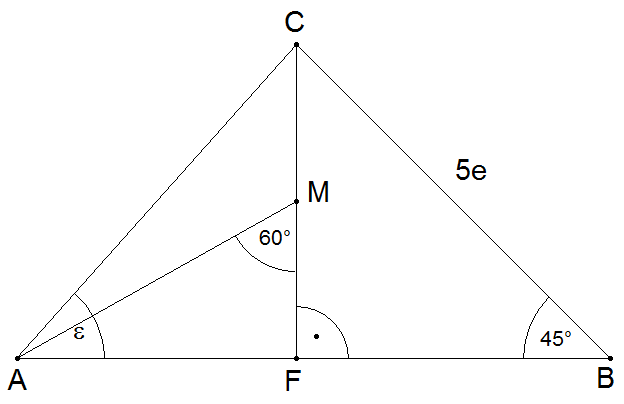
Aufgabe W4b: |
Im
nebenstehenden Dreieck ABC ist M der Mittelpunkt von 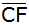 . . |
| |
| Zeigen Sie
ohne Verwendung gerundeter Werte, dass gilt: |
| |
|
|
|
|
 |
3,5
P |
|