|
Pflichtaufgaben |
|
Aufgabe P1: |
|
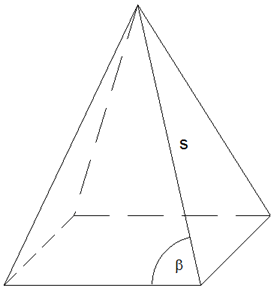
Von einer quadratischen Pyramide sind bekannt: |
| |
 |
|
Berechnen Sie das Volumen der Pyramide. |
|
|
 |
2 P |
|
|
Aufgabe P2: |
| Von einem Kegel
sind bekannt: |
|
|
|
|
| Ein Zylinder
mit gleicher Grundfläche hat das gleich große
Volumen wie der Kegel. |
|
| Berechnen Sie
die Höhe des Zylinders. |
|
|
2 P |
|
|
|
|
Aufgabe P4: |
Gegeben sind
eine nach oben geöffnete Normalparabel mit dem
Scheitelpunkt 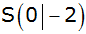 |
und eine
Parabel mit der Gleichung  . . |
| Zeichnen Sie
die beiden Parabeln in ein gemeinsames
Koordinatensystem und berechnen Sie die Koordinaten
ihrer Schnittpunkte. |
|
|
2,5
P |
|
|
Aufgabe P5: |
| Ein Würfel hat
die Kantenlänge a = 6,8 cm. |
| |
| Auf ihm liegt
der Streckenzug PQR mit der Länge 14,9 cm. |
| |
Wie groß ist
der Winkel 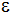 ? ? |
|
|
 |
2 P |
|
|
|
|
Aufgabe P7: |
Im Herbst 2001
betrug der Preis eines Autos 38.900,00 DM. Nach
einer Preiserhöhung im Frühjahr 2002 kostet das Auto
20.505,82  .
(Umrechnung: 1 .
(Umrechnung: 1  =
1,95583 DM) =
1,95583 DM) |
| Um wieviel
Prozent hat sich der Preis des Autos erhöht? |
Der Preis eines
anderen Wagens wurde um den gleichen Prozentsatz
erhöht und stieg damit um 784,58  . . |
| Wie viel Euro
kostet dieser Wagen nach der Preiserhöhung? |
|
|
2 P |
|
|
Aufgabe P8: |
Barbara zahlt
jeweils zu Jahresanfang einen Betrag von 1.200,00  auf
einen Ratensparvertrag ein. Der Zinssatz beträgt
4,5%. Zinsen werden mitverzinst. auf
einen Ratensparvertrag ein. Der Zinssatz beträgt
4,5%. Zinsen werden mitverzinst. |
| Berechnen Sie
das Guthaben nach Ablauf von 3 Jahren. |
Anschließend
lässt sie dieses Guthaben ohne weitere Einzahlung
bei gleichem Zinssatz so lange bei der Bank, bis es
auf 4.000,00  angewachsen
ist. angewachsen
ist. |
| Nach wie viel
Tagen ist dies der Fall? |
|
|
2 P |
|
|
Wahlaufgaben |
|
Aufgabe W1a: |
|
Vom Viereck ABCD sind gegeben: |
| |
 |
Berechnen Sie den Abstand des Punktes D von 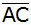 sowie den Winkel CAD.
sowie den Winkel CAD. |
Auf 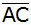 liegt
ein Punkt E; er ist von A und D gleich weit
entfernt. liegt
ein Punkt E; er ist von A und D gleich weit
entfernt. |
Berechnen Sie die Länge von  . . |
|
|
 |
4,5
P |
|
|
Aufgabe W1b: |
|
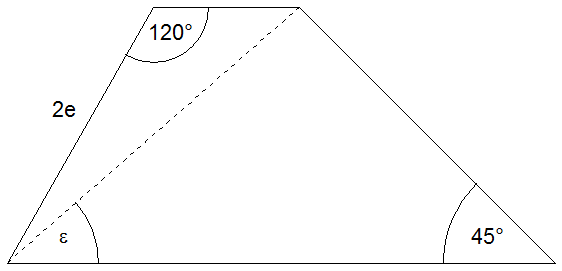
Der Umfang des Trapezes (siehe Skizze) lässt sich
mit der Formel |
| |
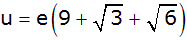 |
berechnen.
|
|
Zeigen Sie ohne Verwendung gerundeter Werte, dass
gilt: |
| |
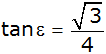 |
|
|
 |
3,5 P |
|
|
Aufgabe W2a: |
Eine Parabel 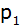 hat
die Gleichung hat
die Gleichung 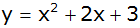 . . |
Eine nach oben
geöffnete Normalparabel 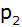 hat
den Scheitelpunkt hat
den Scheitelpunkt  . . |
| |
Bestimmen Sie
rechnerisch die Gleichung der Geraden 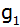 ,
die durch die Scheitelpunkte der beiden Parabeln
geht. ,
die durch die Scheitelpunkte der beiden Parabeln
geht. |
| |
Eine Gerade 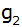 ist
parallel zu ist
parallel zu 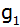 und
geht durch den Schnittpunkt der beiden Parabeln. und
geht durch den Schnittpunkt der beiden Parabeln. |
Berechnen Sie
die Gleichung der Geraden 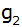 . . |
| |
| Zeichnen Sie
die beiden Parabeln und die beiden Geraden in ein
gemeinsames Koordinatensystem. |
|
|
5 P |
|
|
Aufgabe W2b: |
| Berechnen Sie
die Definitionsmenge und die Lösungsmenge der
Gleichung: |
|
|
|
|
3 P |
|
|
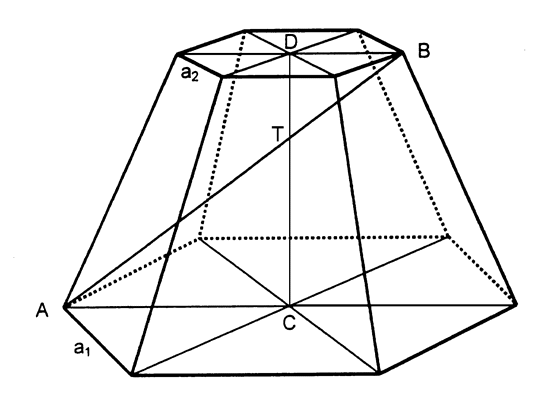
Aufgabe W3a: |
| Von
einem regelmäßigen sechsseitigen Pyramidenstumpf
sind bekannt: |
|
|
Berechnen Sie die Länge der Raumdiagonalen  . . |
|
|
Die
Raumdiagonale  schneidet
die Höhe schneidet
die Höhe 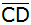 im Punkt T.
im Punkt T. |
|
|
Berechnen Sie die Länge von 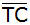 . . |
|
|
 |
4,5
P |
|
|
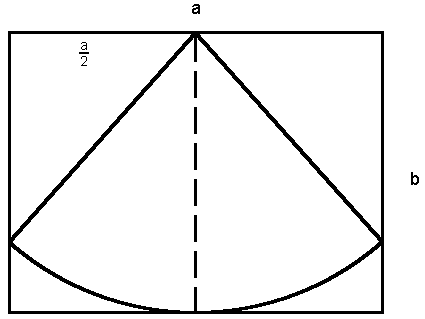
Aufgabe W3b: |
| Aus einem
Rechteck mit den Seiten |
| a = 20,0 cm und
b = 15,0 cm |
| wird ein
Kreisausschnitt ausgeschnitten (siehe Skizze). |
| |
| Der
Kreisausschnitt wird Mantel eines Kegels. |
| |
| Berechnen Sie
das Volumen des Kegels. |
|
|
 |
3,5
P |
|
|
Aufgabe W4a: |
| Lineare und
quadratische Funktionen: Ordnen Sie jedem Schaubild
die richtige |
|
Funktionsgleichung zu und begründen Sie jeweils Ihre
Entscheidung. |
|
|
|
|
4 P |
|
|
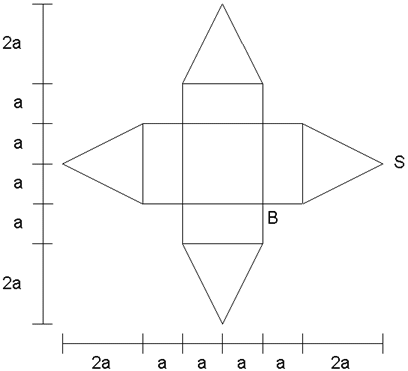
Aufgabe W4b: |
|
Ein Körper hat das dargestellte Netz.
Skizzieren Sie den Körper im
Schrägbild.
Der Flächeninhalt des Netzes beträgt 125 cm².
Berechnen Sie im Körper die Länge der
Strecke 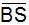 . .
|
|
 |
4 P |
|