Home Geschichte Informatik Lernmaterial Linkliste Mathematik Smartphone ARS LB
2001 Übersicht
nach oben
Pflichtaufgaben
Aufgabe P1:
Ein Kegel und eine Halbkugel sind aus Holz gefertigt.
Der Kegel hat die Maße:
  Grundkreisradius r = 4,2 cm
  Körperhöhe h = 9,5 cm
Die Halbkugel hat die gleich große Oberfläche wie der Kegel.
Berechnen Sie den Radius der Halbkugel.
2 P
Aufgabe P2:
Von einer regelmäßigen fünfseitigen Pyramide sind gegeben:
  Grundkante a = 5,8 cm
  Körperhöhe h = 7,5 cm
Berechnen Sie die Seitenkante s und die Höhe hs einer Seitenfläche.
2 P
Aufgabe P3:
Eine nach oben geöffnete verschobene Normalparabel hat den Scheitelpunkt .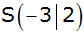
Der Punkt 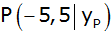 liegt auf der Parabel.
Berechnen Sie die Länge .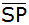
2 P
Aufgabe P4:
Bestimmen Sie die Definitionsmenge und die Lösungsmenge der Gleichung:
 
2,5 P
Aufgabe P5:
Im rechtwinkligen Dreieck ABC gilt:
 
 
 
Wie groß ist ?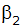
 
Berechnen Sie den Flächeninhalt des Dreiecks BCG.
2 P
Aufgabe P6:
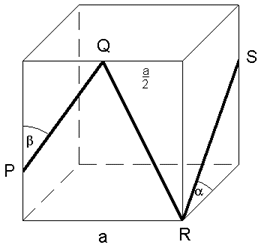
Gegeben ist der Würfel mit der Kantenlänge
a = 7,2 cm.
 
Der Streckenzug PQRS hat die Länge 22,7 cm.
 
Der Winkel 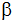 beträgt 37,5°.
 
Berechnen Sie die Länge 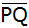 und den
Winkel .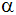
2 P
Aufgabe P7:
Frau Huber legt einen Geldbetrag für drei Jahre bei der Bank an:
  Zinssatz im 1. Jahr: 2,75%
  Zinssatz im 2. Jahr: 3,00%
  Zinssatz im 3. Jahr: 3,50%
Zinsen werden mitverzinst.
 
Am Ende des ersten Jahres werden 206,25 DM Zinsen gutgeschrieben.
 
Wie viel DM Zinsen erhält Frau Huber in den drei Jahren insgesamt?
Um wie viel Prozent erhöht sich das Kapital im Laufe der drei Jahre?
2 P
Aufgabe P8:
In der Europäischen Union hat 1€ (EURO) den Wert:
40,3399 BEF Belgische Franc
1,95583 DEM Deutsche Mark
1 936,27 ITL Italienische Lira
6,55957 FRF Französischer Franc
0,787564 IEP Irisches Pfund
40,3399 LUF Luxemburgischer Franc
166,386 ESP Spanische Peseta
2,20371 NLG Holländischer Gulden
 
 
Der Listenpreis für ein bestimmtes Automodell beträgt in Deutschland 48.900 DEM,
in Frankreich 162.900 FRF.
 
In welchem Land ist das Auto günstiger zu haben?
 
Um wie viel Prozent liegt das günstigere Angebot unter dem ungünstigeren?
 
In Spanien ist das Auto gleich teuer wie in Frankreich.
Wie viele spanische Peseten (ESP) kostet das Auto?
2,5 P
Wahlaufgaben
Aufgabe W1a:
Der Diagonalschnitt eines quadratischen Pyramidenstumpfs hat die Maße:
 
Berechnen Sie die Mantelfläche des Pyramidenstumpfs.
 
Welche Höhe hat die Ergänzungspyramide?
4,5 P
Aufgabe W1b:
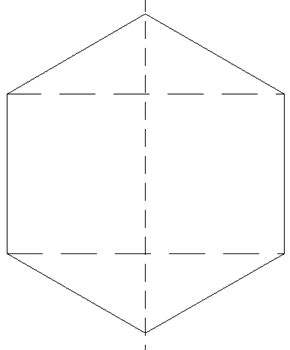
Ein Zylinder mit zwei aufgesetzten Kegeln hat als Achsenschnitt ein regelmäßiges Sechseck mit dem Flächeninhalt
   

Berechnen Sie die Oberfläche des zusammengesetzten Körpers in Abhängigkeit von e ohne Verwendung gerundeter Werte.
3,5 P
Aufgabe W2a:
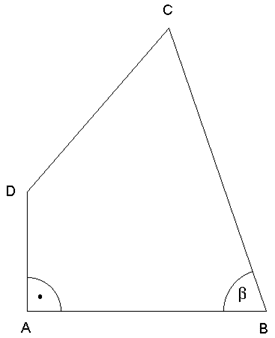
Vom Viereck ABCD sind gegeben:
 
 
Berechnen Sie den Flächeninhalt des Vierecks ABCD sowie den Winkel ADC.
4 P
Aufgabe W2b:
Für das Trapez ABCD gilt:
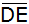liegt parallel zu 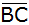und halbiert die Fläche des Trapezes.
Berechnen Sie den Winkel .
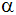4 P
Aufgabe W3a:
Eine Parabel 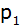hat die Gleichung 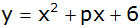und geht durch den Punkt .
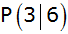Eine Parabel hat die Gleichung und geht durch den Punkt .
  
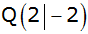Berechnen Sie die Koordinaten der Schnittpunkte der beiden Parabeln.
  
Zeichnen Sie die Parabeln in ein Koordinatensystem.
4 P
Aufgabe W3b:
Eine nach oben geöffnete verschobene Normalparabel wird von der Geraden 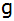in den Punkten
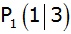und 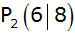geschnitten.
 
Eine zur Geraden 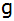parallele Gerade geht durch den Punkt .
 
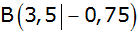Weisen Sie rechnerisch nach, dass der einzige gemeinsame Punkt der Parabel und der Geraden ist.
4 P