Home Geschichte Informatik Lernmaterial Linkliste Mathematik Smartphone ARS LB
2000 Übersicht
nach oben
Pflichtaufgaben
Aufgabe P1:
Eine quadratische Pyramide hat die Maße:
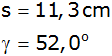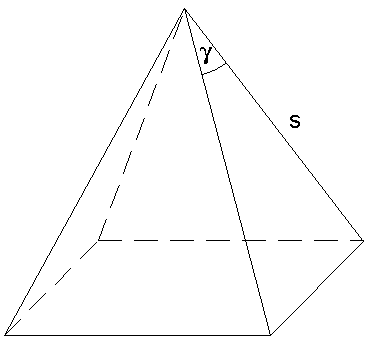
Berechnen Sie das Volumen der Pyramide.
2 P
Aufgabe P2:
Ein massiver Kegel mit dem Durchmesser d = 40,0 cm und der Höhe h = 15,0 cm wird durch einen Schnitt entlang der Höhe halbiert.
 
Berechnen Sie die Oberfläche einer der Kegelhälften.
2,5 P
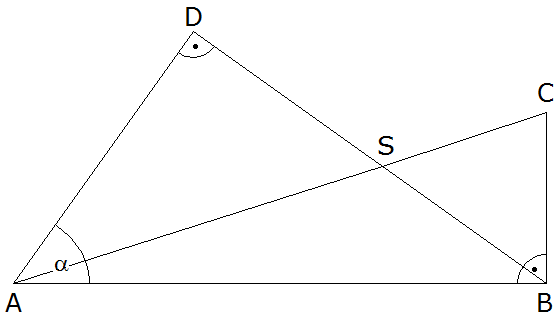
Aufgabe P3:
Für nebenstehende Figur gilt:
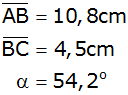Berechnen Sie die Länge .
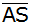2 P
Aufgabe P4:
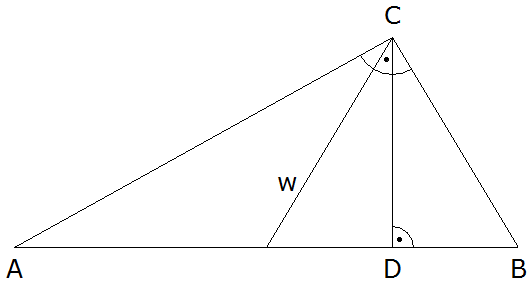
Vom rechtwinkligen Dreieck ABC sind gegeben:
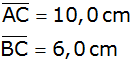Der Winkel ACD wird von halbiert.
Berechnen Sie die Länge von .
2,5 P
Aufgabe P5:
Lösen Sie das Gleichungssystem:
 
2 P
Aufgabe P6:
Eine Parabel hat die Gleichung .
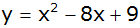Berechnen Sie die Koordinaten des Scheitelpunkts.
  
Diese Parabel wird um 2 Einheiten nach links und um 2,5 Einheiten nach oben verschoben.
Geben Sie die Gleichung der verschobenen Parabel in der Form 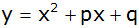an.
2 P
Aufgabe P7:
Doris zahlt drei Jahre hintereinander jeweils zum Anfang des Jahres einen gleich bleibenden
Geldbetrag bei ihrer Bank ein.
Der jährliche Zinssatz beträgt 3,25%.
Zinsen werden mitverzinst.
 
Nach Ablauf der drei Jahre hat sie ein Guthaben von 5438,74 DM.
 
Wie hoch war der jährlich eingezahlte Betrag?
2 P
Aufgabe P8:
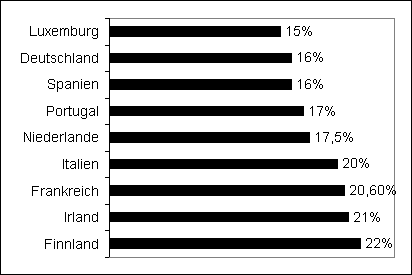
Nebenstehende Grafik zeigt die Prozentsätze der Mehrwertsteuer in einigen Ländern der Europäischen Union (Stand 1.1.1999).
Zu einem Preis von 142,50 Euro kommen 28,50 Euro Mehrwertsteuer hinzu.
In welchem Land ist dies der Fall?
Eine Ware kostet in Luxemburg einschließlich Mehrwertsteuer 172,50 Euro.
Was kostet sie in Irland, wenn der Preis ohne Mehrwertsteuer in beiden Ländern gleich hoch ist?
 
2 P
Wahlaufgaben
Aufgabe W1a:
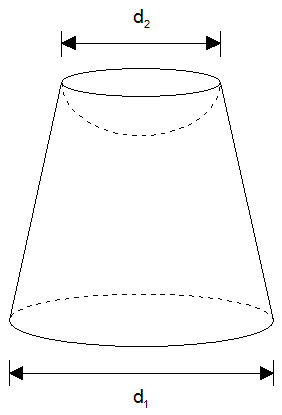
Aus einem Kegelstumpf wurde eine Halbkugel herausgearbeitet.
Für den Restkörper gilt:
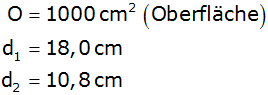Berechnen Sie das Volumen des Restkörpers.
4,5 P
Aufgabe W1b:
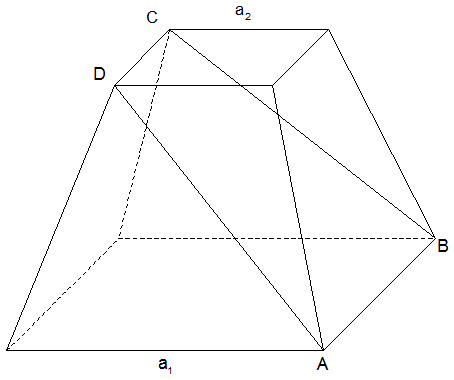
Von einem quadratischen Pyramidenstumpf sind bekannt:
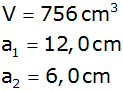Berechnen Sie den Flächeninhalt des Trapezes ABCD.
3,5 P
Aufgabe W2a:
Vom Fünfeck ABCDE sind gegeben:
Berechnen Sie den Abstand des Punktes 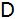von 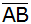und den Winkel .
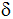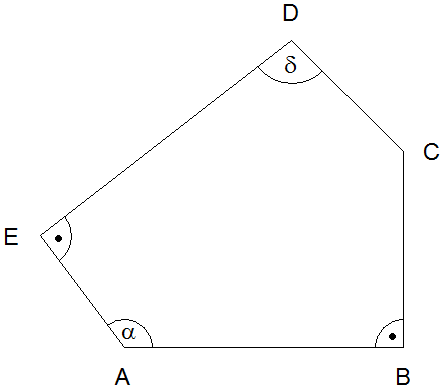5 P
Aufgabe W2b:
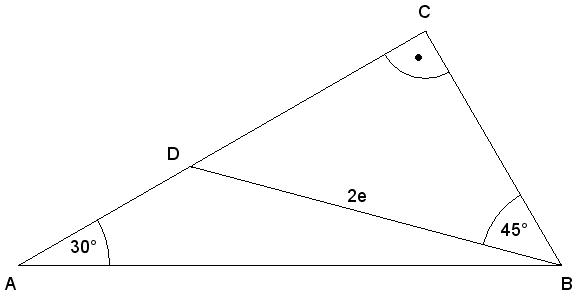
Gegeben ist das Dreieck ABC.
 
Zeigen Sie ohne Verwendung gerundeter Werte, dass sich der Umfang des Teildreiecks ABD mit folgender Formel berechnen lässt:
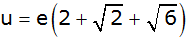3 P
Aufgabe W3a:
Eine nach oben geöffnete Normalparabel 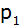hat den Scheitel .
  
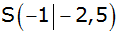Eine weitere Parabel hat die Gleichung .
 
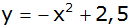Berechnen Sie die Koordinaten der Schnittpunkte von 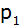und .
  
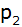Diese Schnittpunkte liegen auf der Geraden .
  
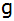Berechnen Sie die Koordinaten des Schnittpunktes der Geraden 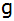mit der x-Achse.
4 P
Aufgabe W3b:
Bestimmen Sie die Definitionsmenge und die Lösungsmenge der Gleichung:
 
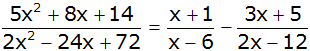4 P