Home Geschichte Informatik Lernmaterial Linkliste Mathematik Smartphone ARS LB
1999 Übersicht
nach oben
Pflichtaufgaben
Aufgabe P1:
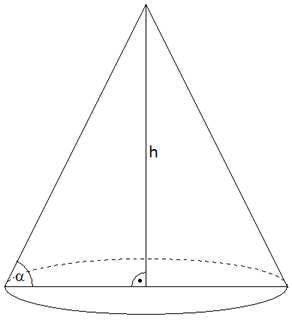
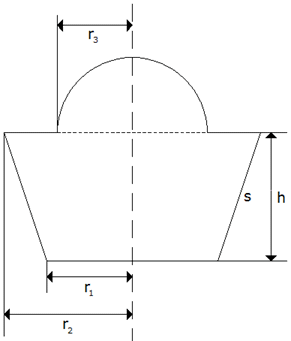
Gegeben ist ein Kegel mit:
Wie groß ist die Oberfläche einer volumengleichen Kugel?
2 P
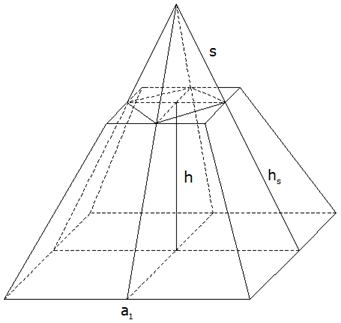
Aufgabe P2:
Der Diagonalschnitt einer quadratischen Pyramide ist ein gleichseitiges Dreieck mit
der Seite s = 8,2 cm.		  
Berechnen Sie die Körperhöhe h, die Grundkante a und die Mantelfläche der Pyramide.
2 P
Aufgabe P3:
Lösen Sie die Gleichung:
2 P
Aufgabe P4:
Eine Parabel hat die Gleichung .
Bestimmen Sie rechnerisch die Koordinaten ihres Scheitelpunktes.
Berechnen Sie die Entfernung des Scheitelpunktes vom Ursprung des Koordinatensystems.
2 P
Aufgabe P5:
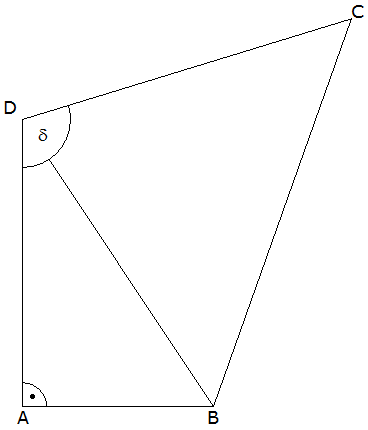
Von der Figur ABCD sind bekannt:
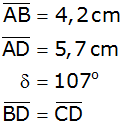Berechnen Sie den Abstand des Punktes 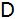von .
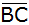2,5 P
Aufgabe P6:
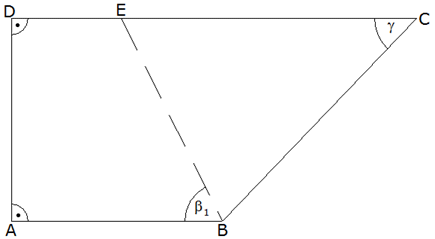
Vom Trapez ABCD sind gegeben:
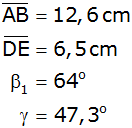Berechnen Sie die Längen und .
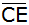2,5 P
Aufgabe P7:
Frau Berg legt bei ihrer Bank am Anfang eines Jahres einen bestimmten Betrag an. Der Zinssatz beträgt 3,75%.
Nach einem Jahr hebt sie 5500,00 DM ab. Nach Ablauf eines weiteren Jahres beträgt ihr Kapital 37350,00 DM. Zinsen werden mitverzinst.
Wie hoch war der ursprünglich angelegte Betrag?
Wie viel DM Zinsen wurden ihr in den beiden Jahren insgesamt gutgeschrieben?
2 P
Aufgabe P8:
Eine Oberbürgermeisterwahl erbrachte folgendes Ergebnis:

Kandidat A Kandidat B Kandidat C
31.751 Stimmen 12.964 Stimmen 8.030 Stimmen
Zahl der ungültigen Stimmen: 796
Wahlbeteiligung: 68,5%
Wie hoch war die Zahl der Wahlberechtigten?
Wie viel Prozent der Wahlberechtigten haben Kandidat A gewählt?
2 P
Wahlaufgaben
Aufgabe W1a:
Von der Figur ABCDE sind gegeben:
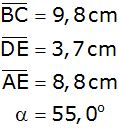Berechnen Sie den Flächeninhalt der Figur.
4,5 P
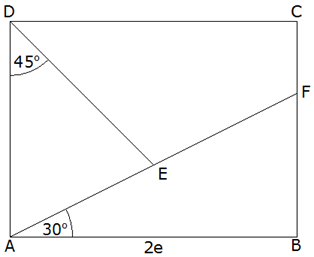
Aufgabe W1b:
Im nebenstehenden Rechteck ABCD halbiert der Punkt 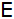die Länge von .
Zeigen Sie ohne Verwendung gerundeter Werte, dass sich der Flächeninhalt des Teildreiecks AED mit der Formel
berechnen lässt.
3,5 P
Aufgabe W2a:
Eine Parabel hat die Gleichung .  
Eine Gerade hat die Gleichung .  
Zeichnen Sie die Parabel und die Gerade in ein Koordinatensystem.
Berechnen Sie die Koordinaten der Schnittpunkte von und .

Diese Schnittpunkte liegen auf einer nach oben geöffneten Normalparabel .
Berechnen Sie die Koordinaten des Scheitelpunktes der Parabel .
5 P
Aufgabe W2b:
Bestimmen Sie die Definitionsmenge und die Lösungsmenge der Gleichung:
3 P
Aufgabe W3a:
Der nebenstehende Achsenschnitt zeigt einen Kegelstumpf mit aufgesetzter Halbkugel.

Gegeben sind:

(Oberfläche des gesamten Körpers)

Berechnen Sie den Radius des Kegelstumpfes und das Volumen der Halbkugel.
4 P
Aufgabe W3b:
Auf einen quadratischen Pyramidenstumpf wird eine quadratische Pyramide aufgesetzt. Die Eckpunkte der Pyramidengrundfläche liegen auf den Seitenmitten der Deckfläche des Stumpfs; und liegen auf einer Geraden.

Für den Pyramidenstumpf gilt:


Geben Sie die Höhe der aufgesetzten Pyramide in Abhängigkeit von an.
4 P