| Pflichtaufgaben |
|
Aufgabe P1: |
Eine nach oben geöffnete Normalparabel hat den
Scheitelpunkt
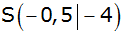 . . |
Berechnen Sie die Koordinaten der Schnittpunkte der
Parabel mit der x-Achse bzw.
der y-Achse. |
|
|
2 P |
|
|
|
|
Aufgabe P3: |
|
Eine quadratische Pyramide hat die Maße: |
|
 |
|
Berechnen Sie die Oberfläche der Pyramide. |
|
|
 |
2,5 P |
|
|
Aufgabe P4: |
Eine
Kugel hat das Volumen
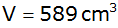 . .
Ihr Radius ist gleich groß
wie der Grundkreisradius eines volumengleichen
Kegels. |
Berechnen Sie die
Mantelfläche des Kegels. |
|
|
2 P |
|
|
Aufgabe P5: |
Die
Entfernung der Punkte
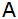 und
und
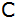 kann nicht direkt gemessen werden. Folgende Größen
sind bekannt:
kann nicht direkt gemessen werden. Folgende Größen
sind bekannt: |
Berechnen Sie die Länge
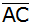 . . |
|
|
 |
2 P |
|
|
Aufgabe P6: |
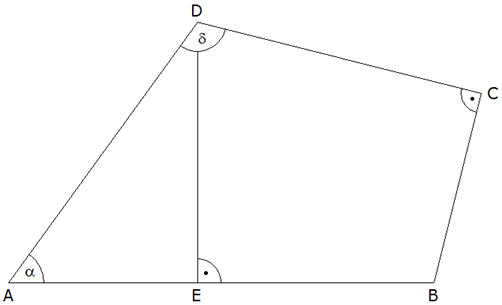
| Vom Viereck
ABCD sind bekannt: |
Berechnen Sie
die Länge
 . . |
|
|
 |
2,5 P |
|
|
Aufgabe P7: |
| Bei einer
Radarkontrolle wurde bei 15% aller Fahrzeuge eine
Geschwindigkeitsübertretung festgestellt. |
| 20 % dieser
Geschwindigkeitsübertretungen führten zu einem
Fahrverbot; das waren 12 Fälle. |
| |
| Wie viele
Fahrzeuge wurden kontrolliert? |
|
|
1,5 P |
|
|
Aufgabe P8: |
Ein Kapital von 24.000,00 DM
wird 5 Jahre lang angelegt. Zinsen werden
mitverzinst.
|
Zinssatz im 1. Jahr: |
3,0% |
|
Zinssatz im 2. Jahr: |
3,5% |
|
Zinssatz im 3. Jahr: |
4,50% |
|
Zinssatz im 4. Jahr: |
6,0% |
|
Für das
fünfte Jahr werden 2.125,55 DM Zinsen
gutgeschrieben. |
|
|
|
| |
|
|
Wie hoch ist der Zinssatz im
fünften Jahr? |
|
| Bei
welchem gleichbleibenden Zinssatz hätte sich nach
fünf Jahren das gleiche Endkapital ergeben? |
|
|
2,5 P |
|
|
Wahlpflichtaufgaben |
|
Aufgabe W1a: |
| Von
einer regelmäßigen achtseitigen Pyramide sind
bekannt: |
|
 |
|
Berechnen Sie die Oberfläche der Pyramide. |
|
|
4 P |
|
|
Aufgabe W1b: |
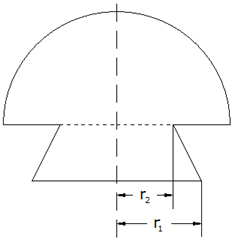
| Ein
zusammengesetzter Körper besteht aus einem
Kegelstumpf und einer Halbkugel.
Es gilt:
|
Zeigen Sie ohne
Verwendung gerundeter Werte, dass sich die
Oberfläche des Körpers mit der Formel
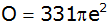
berechnen lässt. |
|
|
 |
4 P |
|
|
Aufgabe W2a: |
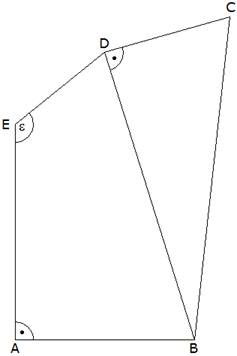
| Vom Viereck
ABDE sind bekannt: |
Berechnen Sie
den Abstand des Punktes D von
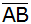 .
Wie groß ist der Winkel AED = .
Wie groß ist der Winkel AED =
 ? ?
Der Flächeninhalt des
Dreiecks BCD ist halb so groß wie der Flächeninhalt
des Vierecks ABDE.
Wie groß ist der Winkel DCB?
|
|
|
 |
5 P |
|
|
Aufgabe W2b: |
| Zeigen Sie ohne
Verwendung gerundeter Werte, dass im nebenstehenden
Dreieck ABC gilt: |
|
|
|
|
 |
3 P |
|
|
Aufgabe W3a: |
Eine Parabel
 mit der Gleichung
mit der Gleichung
 geht durch den Punkt
geht durch den Punkt
 . .
|
|
Eine zweite Parabel
 hat die Gleichung
hat die Gleichung
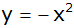 . . |
|
| |
|
Zeichnen Sie beide Parabeln in ein Koordinatensystem
ein.
Berechnen Sie die Koordinaten der
Schnittpunkte der beiden Parabeln.
Bestimmen Sie
rechnerisch die Gleichung der Geraden, die durch
diese beiden Schnittpunkte verläuft. |
|
|
5 P |
|
|
Aufgabe W3b: |
| Bestimmen Sie
die Definitionsmenge und die Lösungsmenge der
Gleichung: |
| |
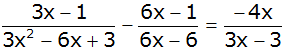 |
|
|
3 P |
|