|
Pflichtaufgaben |
|
Aufgabe P1: |
Eine
quadratische Pyramide mit der Grundkante
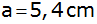 hat die Mantelfläche
hat die Mantelfläche
 . . |
Berechnen
Sie die Höhe
 . .
Wie groß ist der Winkel
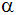 ? ? |
|
|
 |
2,5 P |
|
|
Aufgabe P2: |
Gegeben ist ein Kegel mit dem
Radius
 und dem Volumen
und dem Volumen
 . .
Berechnen Sie seine Oberfläche.
|
|
2 P |
|
|
|
|
Aufgabe P4: |
Eine Parabel
 hat die Gleichung
hat die Gleichung
 . . |
|
| Berechnen Sie
die Koordinaten des Scheitelpunkts und zeichnen Sie
das Schaubild der Parabel. |
|
Die
Parabel
 schneidet eine weitere Parabel
schneidet eine weitere Parabel
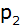 mit der Gleichung
mit der Gleichung
 im Punkt P.
im Punkt P. |
|
| |
|
| Berechnen Sie
die Koordinaten von P. |
|
|
2 P |
|
|
Aufgabe P5: |
| In
der Figur ABCDEF sind gegeben: |
|
 |
Berechnen Sie die Längen
 und
und
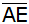 sowie den Winkel
sowie den Winkel
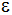 . . |
|
|
 |
2,5 P |
|
|
Aufgabe P6: |
Gegeben ist
die Funktion mit der Gleichung
 . . |
Zeichnen
Sie das Schaubild der Funktion für
 in ein Koordinatensystem
in ein Koordinatensystem
(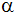 -Achse: -Achse:
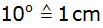 ;
y-Achse: ;
y-Achse:
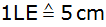 ). ). |
Entnehmen
Sie dem Schaubild (deutliche Kennzeichnung) die
Winkel, für die gilt:
 |
|
|
2 P |
|
|
Aufgabe P7: |
| Frau Jung
schließt einen Ratensparvertrag ab. Sie zahlt
jeweils zu Jahresanfang 2500,00 DM bei ihrer Bank
ein. Der Zinssatz beträgt 3,75%. Zinsen werden
mitverzinst. |
|
Berechnen
Sie das Guthaben nach Ablauf von 3 Jahren. |
|
Wie hoch
hätte Frau Jung die jährlich gleichbleibende Rate
wählen müssen, um bereits nach 2 Jahren bei gleichem
Zinssatz dasselbe Guthaben zu erzielen? |
|
|
2,5 P |
|
|
Aufgabe P8: |
| Frau Müller
legt bei der Bank einen Betrag von 4500,00 DM auf
fünf Jahre zu einem jährlich gleichbleibenden
Zinssatz an. Zinsen werden mitverzinst. Insgesamt
werden in den fünf Jahren 1041,06 DM Zinsen
gutgeschrieben. |
|
Welchen
Zinssatz gewährt die Bank? |
|
|
1,5 P |
|
|
Wahlaufgaben |
|
Aufgabe W1a: |
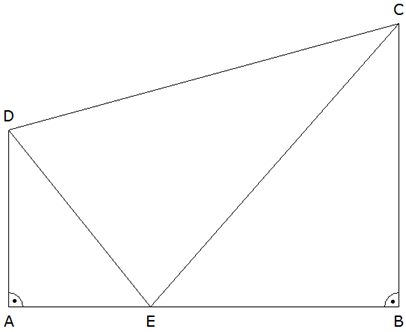
| Im
Viereck ABCD sind gegeben: |
|
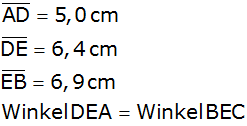 |
|
Berechnen Sie den Winkel DCE. |
|
|
 |
4 P |
|
|
Aufgabe W1b: |
| Im
Dreieck ABC sind gegeben: |
|
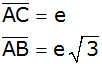 |
Berechnen Sie die Länge
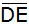 in Abhängigkeit von e (ohne Verwendung gerundeter
Werte).
in Abhängigkeit von e (ohne Verwendung gerundeter
Werte). |
|
Zeigen Sie, daß sich der Flächeninhalt des Dreiecks
DBE mit der Formel |
|
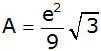 |
|
berechnen läßt. |
|
|
 |
4 P |
|
|
|
|
|
|
Aufgabe W3a: |
|
Eine regelmäßige fünfseitige Pyramide hat die Maße: |
|
 |
|
Sie wird parallel zur Grundfläche so geschnitten,
daß gilt: |
|
 |
Berechnen Sie die
Grundkante
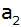 und das Volumen der oberen Pyramide.
und das Volumen der oberen Pyramide. |
|
|
 |
4 P |
|
|
Aufgabe W3b: |
|
Von einem Kegelstumpf sind bekannt: |
|
 |
Aus diesem Kegelstumpf
wird ein Zylinder mit aufgesetzter Halbkugel
herausgearbeitet (siehe nebenstehenden
Achsenschnitt).
Dabei gilt: |
|
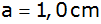 |
|
Um wieviel cm2 ist die Oberfläche des so
entstandenen Körpers größer als die des
ursprünglichen Kegelstumpfes? |
|
|
 |
4 P |
|