|
Aufgabe 1a: |
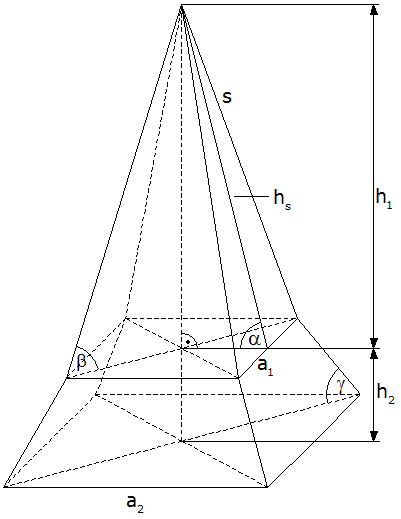
| Das Dach eines
Kirchturmes hat die Form eines quadratischen
Pyramidenstumpfes mit einer aufgesetzten
quadratischen Pyramide. |
Die Maße
sind:
|
|
|
Berechnen Sie
für den pyramidenförmigen Teil des Daches die
Seitenhöhe
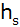 ,
die Seitenkante ,
die Seitenkante
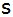 ,
die Mantelfläche ,
die Mantelfläche
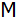 sowie die Neigungswinkel
sowie die Neigungswinkel
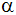 und
und
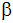 . . |
|
|
 |
4 P |
|
|
Aufgabe 1b: |
| Das Dach eines
Kirchturmes hat die Form eines quadratischen
Pyramidenstumpfes mit einer aufgesetzten
quadratischen Pyramide. |
Die Maße
sind:
|
|
|
Das Volumen des
gesamten Dachraumes beträgt
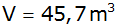 .
Berechnen Sie die Kante .
Berechnen Sie die Kante
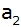 und den Neigungswinkel
und den Neigungswinkel
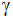 . . |
|
|
 |
4 P |
|
|
Aufgabe 1c: |
| Das Dach eines
Kirchturmes hat die Form eines quadratischen
Pyramidenstumpfes mit einer aufgesetzten
quadratischen Pyramide. |
Für ein
anderes Dach dieser Form gilt:
|
|
|
Zeigen Sie, daß
sich die gesamte Dachfläche mit der Formel
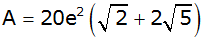 berechnen läßt.
berechnen läßt. |
|
|
 |
3 P |
|
|
|
Aufgabe 2a: |
| Verkehrsflächen
werden durch Pfosten begrenzt. |
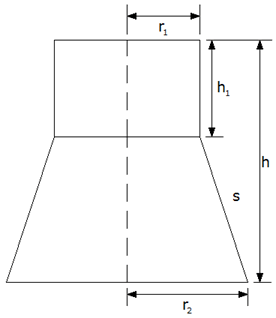
Pfosten I ist aus einem Kegelstumpf und
einem Zylinder zusammengesetzt (s. Achsenschnitt).
|
| Folgende Maße sind
bekannt: |
|
|
|
Berechnen Sie
die Höhe
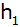 des Zylinders und die Mantellinie
des Zylinders und die Mantellinie
 des Kegelstumpfes. Wie groß ist die Mantelfläche des
zusammengesetzten Körpers in dm2?
des Kegelstumpfes. Wie groß ist die Mantelfläche des
zusammengesetzten Körpers in dm2? |
|
|
 |
4 P |
|
|
Aufgabe 2b: |
| Verkehrsflächen
werden durch Pfosten begrenzt. |
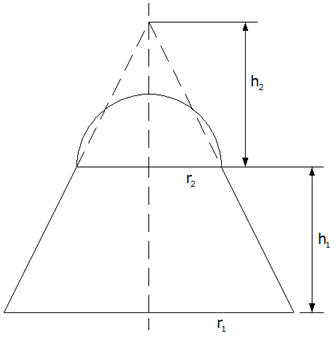
Pfosten II wird wie folgt hergestellt: Ein
Kegel mit dem Volumen
 wird in Höhe
wird in Höhe
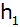 parallel zur Grundfläche geschnitten. Auf die
Schnittfläche wird eine Halbkugel mit gleichem
Radius
parallel zur Grundfläche geschnitten. Auf die
Schnittfläche wird eine Halbkugel mit gleichem
Radius
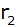 gesetzt (s. Achsenschnitt).
gesetzt (s. Achsenschnitt). |
|
|
Berechnen Sie
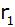 , ,
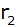 und die Mantelfläche des Pfostens in dm2.
und die Mantelfläche des Pfostens in dm2. |
|
|
 |
4 P |
|
|
Aufgabe 2c: |
| Verkehrsflächen
werden durch Pfosten begrenzt. |
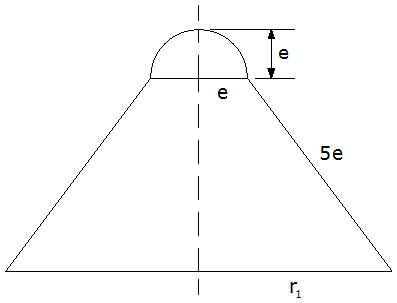
| Für die
Mantelfläche des Pfostens III
(Kegelstumpf mit aufgesetzter Halbkugel) |
|
|
Berechnen Sie
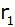 in Abhängigkeit von
in Abhängigkeit von
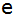 und weisen Sie nach, daß sich das Gesamtvolumen mit
der Formel
und weisen Sie nach, daß sich das Gesamtvolumen mit
der Formel |
|
|
| berechnen läßt. |
|
|
 |
3 P |
|
|
Aufgabe 3a: |
| Ein Grundstück hat
die Maße: |
|
|
|
Berechnen Sie
die Strecken
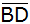 und
und
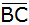 . . |
Welchen Abstand
hat Punkt
 von der Strecke
von der Strecke
 ? ? |
Welchen
Flächeninhalt hat das Grundstück (in
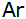 )? )? |
|
|
 |
4 P |
|
|
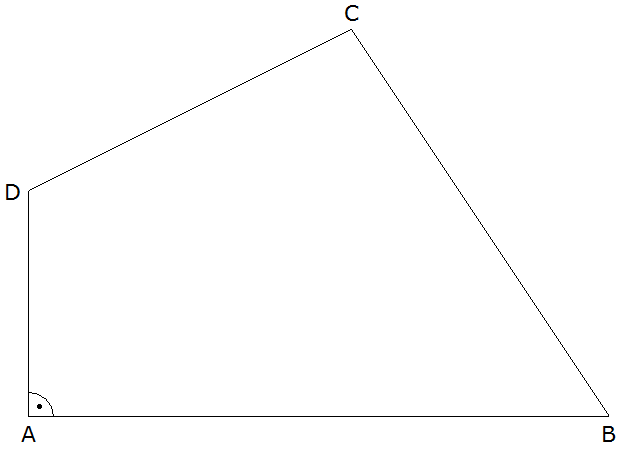
Aufgabe 3b: |
| Für ein anderes
Grundstück gilt: |
|
|
|
Berechnen Sie
die Länge des Lotes von Punkt
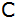 auf die Seite
auf die Seite
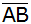 .
Wie lang ist Strecke .
Wie lang ist Strecke
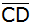 ? ? |
| Wie groß ist
der Winkel ADC? |
|
|
 |
4 P |
|
|
Aufgabe 3c: |
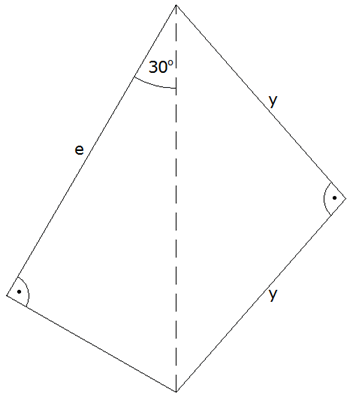
Berechnen Sie für
nebenstehend skizziertes Grundstück die
Seite
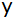 in Abhängigkeit von
in Abhängigkeit von
 .
Zeigen Sie, daß für den Flächeninhalt .
Zeigen Sie, daß für den Flächeninhalt
 gilt:
gilt: |
|
|
|
|
|
 |
3 P |
|
|
Aufgabe 4a: |
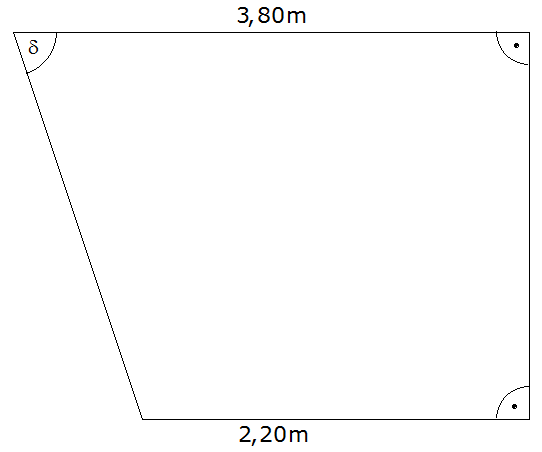
| Es sollen
trapezförmige Platten gefertigt werden. |
| Folgende Maße sind
bekannt: |
|
|
Berechnen Sie die
Höhe
 des Trapezes, seine Seiten
des Trapezes, seine Seiten
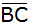 und
und
 sowie die Diagonale
sowie die Diagonale
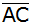 . . |
|
|
|
 |
4 P |
|
|
|
 |
4 P |
|
|
Aufgabe 4c: |
Für
eine Finanzierung werden 48.000,00 DM benötigt.
Die Bank macht folgendes Angebot: |
|
Auszahlungskurs :
96,00%
Zinssatz pro Jahr : 9,25%
bezogen auf die jeweilige Restschuld zu
Jahresanfang
Für Zins und Tilgung sind am Ende
eines jeden Jahres 12.000,00 DM an die Bank zu
zahlen. |
Welcher Betrag muß tatsächlich aufgenommen werden?
Wie hoch ist die Restschuld zu Beginn des vierten
Jahres?
Wieviel Zinsen sind bis dahin insgesamt
bezahlt worden? |
|
|
3 P |
|
|
Aufgabe 5a: |
| Ein Händler hat
verschiedene Helme für Radfahrer im Angebot. |
|
Den Helm A bezieht er für 71,81 DM Er rechnet mit
21,5% Unkosten und einem Gewinn von 26,70 DM pro
Helm. |
Wie hoch ist der Endpreis (einschl. 14% MWSt)?
Wieviel Prozent beträgt der Gewinn bezogen auf den
Selbstkostenpreis?
Um welchen Betrag würde sich
der Endpreis erhöhen, wenn die Mehrwertsteuer auf
15% ansteigen würde? |
|
|
4 P |
|
|
Aufgabe 5b: |
| Ein Händler hat
verschiedene Helme für Radfahrer im Angebot. |
Bei Helm B beträgt der Endpreis 179,90 DM.
Der
Händler kalkuliert dabei wie folgt: |
| |
Unkosten
Gewinn
MWSt |
21% des Bezugspreises
32% der
Selbstkosten
14% des Verkaufspreises |
|
Wie hoch ist der Bezugspreis?
Während einer Werbeaktion setzt der Händler den
Endpreis auf 159,99 DM herab.
Wie hoch ist jetzt
sein Gewinn in DM und in Prozent (die Prozentsätze
für Unkosten und MWSt bleiben unverändert)? |
|
|
4 P |
|
|
Aufgabe 5c: |
| Ein Händler hat
verschiedene Helme für Radfahrer im Angebot. |
Bei Helm C beträgt der Bezugspreis 123,90 DM.
Der Endpreis liegt um 71% über dem Bezugspreis.
Der Betrag des Gewinns ist doppelt so hoch wie
derjenige der Unkosten. |
|
Berechnen Sie die Prozentsätze für Unkosten und
Gewinn. |
|
|
3 P |
|
|
Aufgabe 6a: |
| Familie Neuffer
prüft zwei Möglichkeiten, Geld anzulegen. In beiden
Fällen zahlt die Bank 8,0 % Zinsen jährlich. |
Familie Neuffer möchte 32.000,00 DM vier Jahre lang
anlegen. Sie prüft die Möglichkeit, bei der die
Zinsen
in den Folgejahren mitverzinst werden. |
Auf welchen Betrag ist das Kapital nach vier Jahren
angewachsen?
Um wieviel Prozent hat das Kapital
insgesamt zugenommen?
Wieviel DM Zinsen zahlt die
Bank im vierten Jahr?
Welcher Anfangsbetrag würde
bei diesen Bedingungen nach vier Jahren auf
50.000,00 DM anwachsen? |
|
|
4 P |
|
|
Aufgabe 6b: |
| Familie Neuffer
prüft zwei Möglichkeiten, Geld anzulegen. In beiden
Fällen zahlt die Bank 8,0 % Zinsen jährlich. |
Bei der anderen Möglichkeit werden die Zinsen
jeweils am Jahresende ausbezahlt.
Familie Neuffer
will diese Zinsen dann am Anfang des Folgejahres auf
ein Sparkonto einzahlen, dessen jährlicher
Zinssatz mit 3,5% beginnt und in jedem weiteren Jahr
um 0,5%-Punkte steigt. Zinsen werden mitverzinst. |
Auf welchen Gesamtbetrag wachsen 32.000,00 DM im
Lauf von 4 Jahren an?
Welcher prozentualen
Zunahme entspricht dies insgesamt? |
|
|
4 P |
|
|
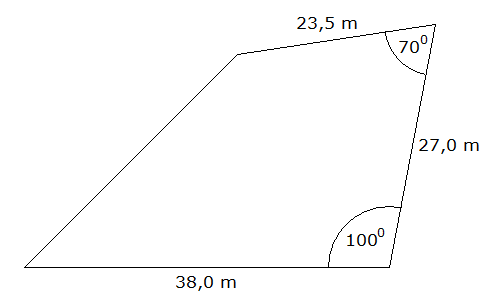
Aufgabe 6c: |
| Familie Neuffer
kauft mit dem angesparten Geld ein Gartengrundstück. |
|
Welchen Flächeninhalt hat das Grundstück? |
|
|
 |
3 P |
|
|