|
Aufgabe 1a: |
Zur Dekoration
von Schaufenstern werden quadratische Pyramiden
(Grundkante
 und Seitenkante
und Seitenkante
 )
aus Kunststoff hergestellt. )
aus Kunststoff hergestellt. |
Berechnen
Sie für eine Pyramide die Seitenhöhe
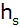 ,
die Körperhöhe ,
die Körperhöhe
 ,
den Neigungswinkel ,
den Neigungswinkel
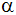 und das Gewicht
und das Gewicht
 in kg, wenn
in kg, wenn
 Material
Material
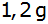 wiegt.
wiegt. |
|
|
 |
4 P |
|
|
Aufgabe 1b: |
Zur Dekoration
von Schaufenstern werden quadratische Pyramiden
(Grundkante
 und Seitenkante
und Seitenkante
 )
aus Kunststoff hergestellt. )
aus Kunststoff hergestellt. |
Eine
dieser Pyramiden wird parallel zur Grundfläche so
durchgeschnitten, dass
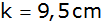 ist.
ist.
Berechnen Sie die
Kantenlänge
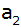 ,
die Mantelfläche und die Höhe des Pyramidenstumpfes. ,
die Mantelfläche und die Höhe des Pyramidenstumpfes. |
|
|
 |
4 P |
|
|
Aufgabe 1c: |
Zur Dekoration
von Schaufenstern werden zwei verschiedene quadratische Pyramidenstümpfe
aus Kunststoff
hergestellt. |
|
Typ I: |
Grundkante
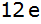 ,
Deckkante ,
Deckkante
 und Körperhöhe
und Körperhöhe
 . .
Zeigen Sie, dass das Volumen eines solchen
Pyramidenstumpfes
 beträgt.
beträgt. |
|
|
Typ II: |
Grundkante
 ,
Körperhöhe ,
Körperhöhe
 und Volumen
und Volumen
 . .
Berechnen Sie die Deckkante in
Abhängigkeit von
 . . |
|
|
|
3 P |
|
|
Aufgabe 2a: |
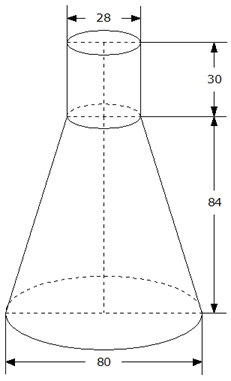
| Eine Firma
stellt oben offene Behälter aus Stahlblech her. Sie
haben die Form eines Kegelstumpfes mit aufgesetztem
Zylinder. |
Wieviel
Liter fasst der Behälter?
Aus wievielen
Quadratmetern Stahlblech besteht er?
Maße in cm! |
|
|
 |
4 P |
|
|
Aufgabe 2b: |
| Eine Firma
stellt oben offene Behälter aus Stahlblech her. Sie
haben die Form eines Kegelstumpfes mit aufgesetztem
Zylinder. |
| Ein anderer
Behälter erhält gemäß nebenstehender Abbildung ein
Überlaufrohr. Er kann bis zu diesem Rohr mit 329
Litern gefüllt werden. |
| Berechnen Sie
den oberen Durchmesser der Füllung und die Strecke
x. Maße in cm! |
|
|
 |
4 P |
|
|
Aufgabe 2c: |
| Für das Preisangebot erstellt die
Firma folgende Kalkulation: |
| Herstellungskosten 1.700,00 DM,
Unkosten 24% der Herstellungskosten. Dazu kommen Gewinn und
14% Mehrwertsteuer. |
| Der Endpreis im Angebot beträgt
3.076,00 DM einschl. MWSt. |
Die Firma muss einen Teil der
anfallenden Kosten durch Überziehen ihres Girokontos
vorfinanzieren. Der Überziehungsbetrag von 2.000,00 DM wird
105 Tage in Anspruch genommen. Die Bank rechnet mit einem
Zinssatz von 9,5% pro Jahr. |
| Berechnen Sie den tatsächlichen
Gewinn in DM. |
|
3 P |
|
|
Aufgabe 3a: |
Bei einem
Geländespiel sollen Schüler vom Start
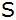 zum Ziel
zum Ziel
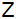 (
(
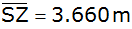 ) gehen. Vom Punkt
) gehen. Vom Punkt
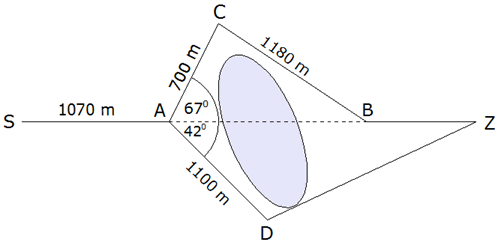
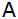 aus muss ein See umgangen werden (siehe Wegskizze).
aus muss ein See umgangen werden (siehe Wegskizze). |
Eine
Schülergruppe erreicht über die Punkte
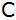 und
und
 das Ziel
das Ziel
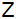 . . |
| Zeichnen Sie
das Dreieck ABC im Maßstab 1 : 10.000. |
Berechnen Sie
den Winkel CBA, die Strecke
 und die zurückgelegte Gesamtstrecke.
und die zurückgelegte Gesamtstrecke. |
|
|
 |
4 P |
|
|
Aufgabe 3b: |
Bei einem
Geländespiel sollen Schüler vom Start
 zum Ziel
zum Ziel
 (
(
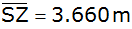 ) gehen. Vom Punkt
) gehen. Vom Punkt
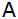 aus muss ein See umgangen werden (siehe Wegskizze).
aus muss ein See umgangen werden (siehe Wegskizze). |
Eine andere
Schülergruppe umgeht den See von
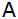 über Punkt
über Punkt
 . . |
| Welche
Gesamtstrecke legt diese Gruppe zurück? |
Um wie viele
Meter wäre der Weg dieser Gruppe kürzer, wenn sie
vom Start
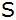 direkt über den Punkt
direkt über den Punkt
 zum Ziel
zum Ziel
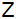 gehen würde?
gehen würde? |
| Wie groß wäre
dabei Winkel DSA? |
|
|
 |
4 P |
|
|
Aufgabe 3c: |
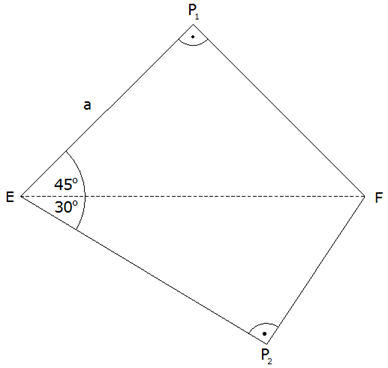
Zeigen Sie,
dass für die Länge des Weges von
 über
über
 nach
nach
 gilt:
gilt: |
|
|
|
|
 |
3 P |
|
|
Aufgabe 4a: |
| Für ein
Schulfest bauen Schüler Marktstände. |
|
Die Skizze zeigt eine geplante Seitenwand (Maße in
cm). |
Berechnen Sie die Strecke
 ,
den Winkel ,
den Winkel
 und die Strecke
und die Strecke
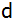 . . |
|
Wie groß ist die Gesamtfläche des Vierecks ABCD in
Quadratmetern? |
|
|
 |
4 P |
|
|
Aufgabe 4b: |
| Für ein
Schulfest bauen Schüler Marktstände. |
|
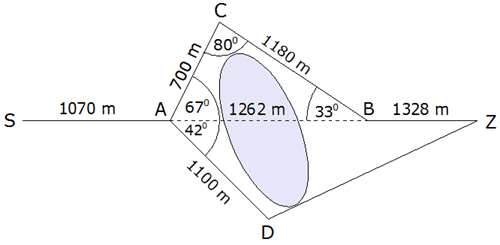
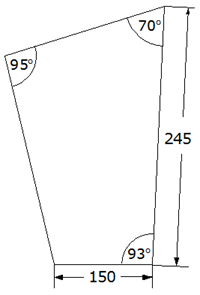
Die Wand eines anderen Standes hat die in der Skizze
angegebenen Maße (in cm). |
|
Berechnen Sie den Umfang dieser Wand. |
|
|
 |
4 P |
|
|
Aufgabe 4c: |
| Für ein
Schulfest bauen Schüler Marktstände. |
Geben Sie bei der nebenstehenden skizzierten Wand
ABCD die Länge von
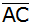 in Abhängigkeit von
in Abhängigkeit von
 an.
an. |
|
Zeigen Sie, dass für die Fläche der Wand gilt: |
|
|
|
|
 |
3 P |
|
|
Aufgabe 5a: |
| Fahrradhändler
Drais bezieht eine Lieferung von 30 Fahrrädern zum Preis von
je 330,00 DM. Er kalkuliert mit Unkosten von 35% des
Bezugspreises, mit einem Gewinn von 8% der Selbstkosten und
14% Mehrwertsteuer (MWSt). |
| Welcher
Endpreis ergibt sich für ein Fahrrad? |
| 20 Fahrräder
verkauft Herr Drais zu diesem Preis, 10 zu einem Sonderpreis
von je 500,00 DM (einschließlich MWSt). |
| Wieviel nimmt
Herr Drais insgesamt ein? |
| Wieviel DM
Mehrwertsteuer sind in diesem Betrag enthalten? |
|
|
4 P |
|
|
Aufgabe 5b: |
| Im Jahr 1983
hatte der Fahrradhändler Einnahmen von 72.800,00 DM. Er ging
damals von einem jährlichen gleichbleibenden Zuwachs der
Einnahmen von 12% aus. |
| Wie hoch hätten
nach dieser Prognose die Einnahmen im Jahr 1988 sein müssen? |
| Tatsächlich
ergaben sich folgende Wachstumsraten (jeweils bezogen auf
das Vorjahr): 18% Zuwachs (1984), 4% Abnahme (1985) und 21%
Zuwachs (1986). 1988 ergab sich die gleiche Wachstumsrate
wie 1987. |
| Wie hoch war
die Wachstumsrate (in %) für 1988 bzw. 1987, wenn Herr Drais
1988 93.800,00 DM eingenommen hatte? |
| Welcher
gleichbleibenden Wachstumsrate für die letzten drei Jahre
(1986 bis 1988) würde dies entsprechen? |
|
|
4 P |
|
|
Aufgabe 5c: |
| Zeigen Sie,
dass für einen Bezugspreis von 500,00 DM pro Fahrrad,
Unkosten von 40% und einem Gewinn von x% (bezogen auf die
Selbstkosten) der Endpreis E (einschließlich MWSt) mit der
Formel |
|
|
| berechnet
werden kann. |
| Mit welchem
Gewinn (in %) kalkuliert Herr Drais bei einem Endpreis von
957,60 DM? |
| Er gewährt 3%
Rabatt. Wie hoch ist jetzt der Gewinn (in %)? |
|
|
3 P |
|
|
Aufgabe 6a: |
| Firma
Feuerstein hat einen Tank für 250.000 Liter Heizöl. Als er
gefüllt wurde, betrug der Ölpreis 24,00 DM pro 100 Liter
zuzüglich 14% Mehrwertsteuer. |
| Wieviel musste
die Firma für die Füllung bezahlen? |
| Als 60% des
Ölvorrats verbraucht sind, wird der Tank wieder gefüllt. |
| Was kostet
dies, wenn der Ölpreis um 8,5% gestiegen ist? |
| Der gesamte
Tankinhalt reicht für 125 Tage. |
| Wie hoch ist
der durchschnittliche Tagesverbrauch? |
| Durch
Produktionssteigerung erhöht sich dieser Tagesverbrauch um
25%. |
| Wie lange
reicht der gesamte Tankinhalt nun? |
|
|
4 P |
|
|
Aufgabe 6b: |
| Die Erweiterung
des Tanklagers der Firma Feuerstein kostet 210.000 DM.
Dieser Betrag wird zu 35% aus Rücklagen aufgebracht. Der
Rest wird durch ein Darlehen finanziert. Für Zins und
Tilgung werden jährlich gleichbleibend zusammen 19.000 DM
geleistet, wobei das jeweilige Restdarlehen mit 7% verzinst
wird. |
| Geben Sie in
einer Tabelle für 4 Jahre die Zins- und Tilgungsanteile pro
Jahr an. |
| Wieviel Prozent
des ursprünglichen Darlehens sind nach 4 Jahren getilgt? |
|
|
4 P |
|
|
Aufgabe 6c: |
3 P |
| Ein neuer Tank hat die Form eines
Zylinders mit einer Höhe von 4,0 m und einem Durchmesser von
7,0 m. |
Eine kegelstumpfförmige
Auffangwanne, die im Schadensfall den vollen Tankinhalt
aufnehmen muss, soll
innen mit einem Schutzanstrich
versehen werden.
Wieviel Quadratmeter Fläche sind zu
streichen, wenn die Wanne 1,0 m hoch ist und ihr unterer,
kleinerer
Durchmesser 9,0 m beträgt? |
|
|